题目内容
14. 如图所示,质量分别为m和2m的两个小球置于光滑水平面上,且固定在一轻质弹簧的两端,现沿弹簧轴线方向在质量为2m的小球上施加一水平向右的拉力F1,使两球一起做匀加速运动,则此时两球间的距离为x1,若沿弹簧轴线方向在质量为m的小球上施加一水平向左的拉力F2,使两球一起做匀加速运动,则此时两球间的距离为x2,已知x1=2x2,则有( )
如图所示,质量分别为m和2m的两个小球置于光滑水平面上,且固定在一轻质弹簧的两端,现沿弹簧轴线方向在质量为2m的小球上施加一水平向右的拉力F1,使两球一起做匀加速运动,则此时两球间的距离为x1,若沿弹簧轴线方向在质量为m的小球上施加一水平向左的拉力F2,使两球一起做匀加速运动,则此时两球间的距离为x2,已知x1=2x2,则有( )| A. | F1=F2 | B. | F1=4F2 | C. | F1>4F2 | D. | F1=2F2 |
分析 对整体分析,根据牛顿第二定律求出整体的加速度,隔离分析,结合牛顿第二定律求出弹簧的弹力,从而根据胡克定律求出弹簧的形变量,得出两球之间的距离.
解答 解:设弹簧的原长为l,沿弹簧轴线方向在质量为2m的小球上施加一水平向右的拉力F1,对整体分析,整体的加速度a=$\frac{{F}_{1}}{3m}$,
隔离对m的小球分析,根据牛顿第二定律得,${F}_{弹}=ma=\frac{{F}_{1}}{3}=k{(x}_{1}-l)$;
同理,沿弹簧轴线方向在质量为m的小球上施加一水平向左的拉力F2,a′=$\frac{{F}_{2}}{3m}$,
隔离对2m的小球分析,根据牛顿第二定律得:${F}_{弹}′=2ma′=\frac{2{F}_{2}}{3}=k{(x}_{2}-l)$
由于x1=2x2,
联立可得:F1>4F2,故C正确,ABD错误;
故选:C.
点评 本题考查了牛顿第二定律和胡克定律的综合运用,知道两球具有相同的加速度,结合牛顿第二定律进行求解,掌握整体法和隔离法的灵活运用.

练习册系列答案
相关题目
5. 如图a所示,将质量为m的物体置于倾角为θ的平板上,当θ从0缓慢增大到90°的过程中,物体所受摩擦力Ff与θ的关系如图b所示,已知物体始终没有脱离平板,物体与平板间的动摩擦因数为0.75.最大静摩擦力与滑动摩擦力相等,重力加速度为g,则( )
如图a所示,将质量为m的物体置于倾角为θ的平板上,当θ从0缓慢增大到90°的过程中,物体所受摩擦力Ff与θ的关系如图b所示,已知物体始终没有脱离平板,物体与平板间的动摩擦因数为0.75.最大静摩擦力与滑动摩擦力相等,重力加速度为g,则( )
 如图a所示,将质量为m的物体置于倾角为θ的平板上,当θ从0缓慢增大到90°的过程中,物体所受摩擦力Ff与θ的关系如图b所示,已知物体始终没有脱离平板,物体与平板间的动摩擦因数为0.75.最大静摩擦力与滑动摩擦力相等,重力加速度为g,则( )
如图a所示,将质量为m的物体置于倾角为θ的平板上,当θ从0缓慢增大到90°的过程中,物体所受摩擦力Ff与θ的关系如图b所示,已知物体始终没有脱离平板,物体与平板间的动摩擦因数为0.75.最大静摩擦力与滑动摩擦力相等,重力加速度为g,则( )| A. | O-q段图线是直线 | B. | q-$\frac{π}{2}$段图线是直线 | ||
| C. | P=$\frac{3mg}{5}$ | D. | q=$\frac{π}{6}$ |
2.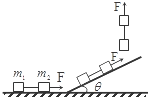 如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )
如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )
 如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )
如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )| A. | 由大变小 | B. | 由小变大 | ||
| C. | 始终不变且大小为$\frac{m}{{m}_{1}+{m}_{2}}$F | D. | 由大变小再变大 |
9.在空中下落的物体,由于空气阻力随着速度的增大而增大,最终会达到一个恒定的速度,称之为收尾速度.一物体质量为m,将它从空中静止释放,最后物体的收尾速度为v,重力加速度为g,下列说法正确的是( )
| A. | 若测得物体从释放至达到收尾速度所用时间为t,则物体下落的位移为$\frac{vt}{2}$ | |
| B. | 若测得某一时刻物体下落时的加速度为a,则物体此时的速度为$\sqrt{2ah}$ | |
| C. | 若测得某时物体的加速度为a,此时物体受到的空气阻力为mg-ma | |
| D. | 若测得物体下落t时间,通过的位移为y,则该过程的平均速度一定为$\frac{y}{t}$ |
19. 滑板A放在光滑水平面上,质量为M,质量为m的滑块B(可视为质点)放在滑板右端,滑块与滑板间动摩擦因数为μ,滑板和滑块均静止.现对滑板施加向右的水平恒力F,滑块从滑板右端滑到左端的时间为t.下列判断正确的是( )
滑板A放在光滑水平面上,质量为M,质量为m的滑块B(可视为质点)放在滑板右端,滑块与滑板间动摩擦因数为μ,滑板和滑块均静止.现对滑板施加向右的水平恒力F,滑块从滑板右端滑到左端的时间为t.下列判断正确的是( )
 滑板A放在光滑水平面上,质量为M,质量为m的滑块B(可视为质点)放在滑板右端,滑块与滑板间动摩擦因数为μ,滑板和滑块均静止.现对滑板施加向右的水平恒力F,滑块从滑板右端滑到左端的时间为t.下列判断正确的是( )
滑板A放在光滑水平面上,质量为M,质量为m的滑块B(可视为质点)放在滑板右端,滑块与滑板间动摩擦因数为μ,滑板和滑块均静止.现对滑板施加向右的水平恒力F,滑块从滑板右端滑到左端的时间为t.下列判断正确的是( )| A. | 滑块与滑板间动摩擦因数应满足$μ<\frac{F}{Mg}$ | |
| B. | 若仅减小M,时间t会缩短 | |
| C. | 若仅减小m,时间t会缩短 | |
| D. | 若仅减小F,时间t会缩短 | |
| E. | 若在滑板A右端与B平齐地再放一个同样的滑块C,则两滑块在滑板上的运动时间t不变 |
6. 如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
 如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )| A. | 若加速度足够小,竖直挡板对球的弹力可能为零 | |
| B. | 若加速度足够大,斜面对球的弹力可能为零 | |
| C. | 斜面对球的弹力大小与加速度大小无关 | |
| D. | 挡板对球的弹力大小与加速度大小无关 |
11. 如图所示,水平地面上固定一足够长的光滑斜面(空气阻力不计),质量为m的小球以初速度v0从斜面底端冲上斜面,在小球沿斜面向上运动的过程中( )
如图所示,水平地面上固定一足够长的光滑斜面(空气阻力不计),质量为m的小球以初速度v0从斜面底端冲上斜面,在小球沿斜面向上运动的过程中( )
 如图所示,水平地面上固定一足够长的光滑斜面(空气阻力不计),质量为m的小球以初速度v0从斜面底端冲上斜面,在小球沿斜面向上运动的过程中( )
如图所示,水平地面上固定一足够长的光滑斜面(空气阻力不计),质量为m的小球以初速度v0从斜面底端冲上斜面,在小球沿斜面向上运动的过程中( )| A. | 小球以速度v0沿斜面做匀速直线运动 | |
| B. | 小球受到重力、斜面的支持力、沿斜面向上的冲力 | |
| C. | 小球受到的支持力大小为mgsinθ | |
| D. | 小球受到的支持力大小为mgcosθ |
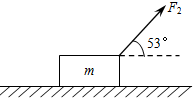 质量m=20kg的木箱放在水平地面上,木箱与地面之间的动摩擦因数μ=0.5.若用水平力F1拉木箱,木箱恰好做匀速直线运动;若用F2=150N、与水平方向成53°斜向上的拉力作用于静止的木箱上,如图所示,作用时间4s后撤去F2.求:
质量m=20kg的木箱放在水平地面上,木箱与地面之间的动摩擦因数μ=0.5.若用水平力F1拉木箱,木箱恰好做匀速直线运动;若用F2=150N、与水平方向成53°斜向上的拉力作用于静止的木箱上,如图所示,作用时间4s后撤去F2.求: 如图,用两根绳子把质量为10千克的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,如果绳子的质量忽略不计,求A处和B处所受力的大小.
如图,用两根绳子把质量为10千克的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,如果绳子的质量忽略不计,求A处和B处所受力的大小.