题目内容
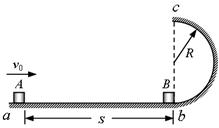
如图所示，半径R = 0.1m的竖直半圆形光滑轨道bc与水平面ab相切。
质量m = 0.1㎏的小滑块B放在半圆形轨道末端的b点，另一质量也为m =
0.1kg的小滑块A，以v0 =
2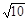
m/s的水平初速度向B滑行，滑过s = 1m的距离，与B相碰，碰撞时间极短，碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求
（1）A与B碰撞前瞬间的速度大小vA；
（2）碰后瞬间，A与B共同的速度大小v；
（3）在半圆形轨道的最高点c，轨道对A与B
的作用力N的大小。
【答案】
（1）
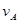=6m/s
（2）v=3m/s
（3）N=8N
【解析】（1）滑块做匀减速直线运动，加速度大小：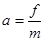
=2 m/s2
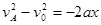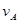解得：=6m/s
（2）碰撞过程中满足动量守恒：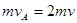
解得：v=3m/s
（3）由b运动到a的过程中，根据动能定理
设a点的速度为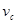
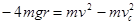解得：=
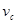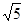m/s
根据受力分析: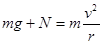
解得：N=8N
练习册系列答案
阅读快车系列答案
相关题目
如图所示，半径R=0.8m的光滑绝缘导轨固定于竖直平面内，加上某一方向的匀强电场时，带正电的小球沿轨道内侧做圆周运动．圆心O与A点的连线与竖直成一角度θ，在A点时小球对轨道的压力N=120N，此时小球的动能最大．若小球的最大动能比最小动能多32J，且小球能够到达轨道上的任意一点（不计空气阻力）．则：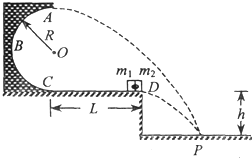
如图所示，半径R=0.5m的光滑半圆轨道竖直固定在高h=0.8m的光滑水平台上，与平台平滑连接，平台长L=1.2m．可视为质点的两物块m1、m2紧靠在一起静止于平台的最右端D点，它们之间有烈性炸药．现点燃炸药，假设炸药释放出来的能量全部转化为物块m1、m2的机械能，且它们只具有水平方向的速度．m1通过平台到达半圆轨道的最高点A时，轨道对它的压力大小是N=44N，水平抛出后在水平地面上的落点与m2的落点相同．已知m1=2kg，g取10m/s2．求：
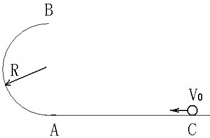如图所示，半径R=0.4m的光滑半圆轨道处于竖直平面内，半圆环与粗糙的水平地面相切于圆环的端点A，一质量m=0.1kg的小球，以初速度v0=8.0m/s，从C点起在水平地面上向左运动，经A点冲上半圆轨道恰好通过轨道最高点B后水平抛出，求：（取重力加速度g=10m/s2）
如图所示，半径r=0.5m的光滑圆轨道被竖直固定在水平地面上，圆轨道最低处有一小球（小球的半径比r小很多）．现给小球一个水平向右的初速度V0，要使小球不脱离轨道运动，V0应满足（ ）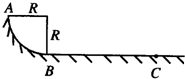
如图所示，半径R=1m的1/4圆弧导轨与水平面相接，从圆弧导轨顶端A，静止释放一个质量为m=20g的小木块，测得其滑至底端B时速度VB=3m/s，以后沿水平导轨滑行BC=3m而停止．