题目内容
如图所示,电荷量均为+q、质量分别为m和
(1)电场的场强及细绳断开后A、B两球的加速度;
(2)当B球速度为零时,A球的速度大小;
(3)自绳断开至B球速度为零的过程中,两球组成系统的机械能增量为多少?
解:(1)设电场强度为E,把小球A、B看做一个系统,由于绳未断前做匀速运动,则有:2qE=4mg;E=![]() ①
①
细绳断后,根据牛顿第二定律,得:qE-mg=maa aa=g,方向向上;②
qE-3mg=3mab ab=-![]() (负号表示方向向下)。③
(负号表示方向向下)。③
(2)细绳断开前后两绳组成的系统满足合外力为零,所以系统总动量守恒。设B球速度为零时,A球的速度为va,根据动量守恒定律,得:(m+
(3)设自绳断开到球B速度为零的时间为t,则:0=v+abt,ab=-![]() 得t=
得t=![]() ⑤
⑤
在该时间内A的位移为:
sa=![]()
由功能关系知,电场力对A做的功等于物体A的机械能增量:ΔEa=qEsa=2mg·![]() =15mv2⑥
=15mv2⑥
同理,研究B得:ΔEb=qEsb=2mg·![]() =3mv2⑦
=3mv2⑦
所以:ΔE=ΔEa+ΔEb=18mv2⑧

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图所示,电荷量均为+q、质量分别为m和2m的小球A和B.中间连接质量不计的细绳,在竖直方向的匀强电场中以速度v0匀速上升,某时刻细绳断开(不考虑电荷间的库仑力作用),求:
如图所示,电荷量均为+q、质量分别为m和2m的小球A和B.中间连接质量不计的细绳,在竖直方向的匀强电场中以速度v0匀速上升,某时刻细绳断开(不考虑电荷间的库仑力作用),求: 如图所示,电荷量均为+q、质量分别为m和3m的小球A和B,中间连接质量不计的细绳,在竖直方向的匀强电场中以速度v0匀速上升.若不计两带电小球间的库仑力作用,某时刻细绳断开,求:
如图所示,电荷量均为+q、质量分别为m和3m的小球A和B,中间连接质量不计的细绳,在竖直方向的匀强电场中以速度v0匀速上升.若不计两带电小球间的库仑力作用,某时刻细绳断开,求: 如图所示,电荷量均为+Q的点电荷A、B连线上有a、c两点,在连线的中垂线上有b、d两点,a、b、c、d点都与连线的中点O等距.下列说法中正确的是( )
如图所示,电荷量均为+Q的点电荷A、B连线上有a、c两点,在连线的中垂线上有b、d两点,a、b、c、d点都与连线的中点O等距.下列说法中正确的是( )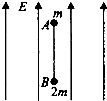 如图所示,电荷量均为+q、质量分别为m和2m的小球A和B,中间连接质量不计的绝缘细绳(不考虑电荷之间的库仑力),在竖直方向的匀强电场中以速度v0匀速上升,某时刻细绳断开.求:
如图所示,电荷量均为+q、质量分别为m和2m的小球A和B,中间连接质量不计的绝缘细绳(不考虑电荷之间的库仑力),在竖直方向的匀强电场中以速度v0匀速上升,某时刻细绳断开.求: