题目内容
如图所示的直角坐标系xoy中,在x<0,y>0的区域有一对平行金属板M和N,其中N板位于x轴上,M、N板加有如图所示电压,平行金属板右侧存在沿y轴负向与平行金属板等宽度的匀强电场,场强大小为E,在x>0 y>0的区域存在垂直纸面的矩形有界磁场,其下边界和左边界分别与Ox、Oy轴重合.t=0时刻一质量为m,电量为q的带电微粒沿着平金属板的轴线O1O 2以初速度v0向右开始运动,恰从M板右边缘的P点沿x轴正向进入平行金属板右侧电场,经过一段时间后以2v0的速度经Q点进入磁场,Q点为O1O2与y轴的交点,再经磁场偏转带电微粒恰好从坐标原点O沿x轴负向返回电场,不计带电微粒的重力.求:
(1)平行金属板M、N间的距离d及右侧电场的宽度L;
(2)平行金属板上所加电压U0满足的条件;
(3)矩形磁场区域的最小面积.

(1)平行金属板M、N间的距离d及右侧电场的宽度L;
(2)平行金属板上所加电压U0满足的条件;
(3)矩形磁场区域的最小面积.

分析:(1)研究带电粒子从P运动到Q的地过程:带电粒子做类平抛运动,初速度为v0,到达Q点的速度为2v0,即可求得Q点的速度与水平方向的夹角,得到竖直方向的分速度vy,
=2?(
)?
,L=v0t,求得d和L.
(2)由题意,画出带电粒子在平行金属板间的运动轨迹,粒子在电场中运动的侧向总位移应满足:
=
?
?(
)2?2n,其中n=1,2,3,…,L=v0?nT,即可求出电压U0满足的条件;
(3)画出带电粒子在磁场中的运动轨迹,由几何知识求出最小矩形磁场的长和宽,即可求出磁场的最小面积.
| v | 2 y |
| qE |
| m |
| d |
| 2 |
(2)由题意,画出带电粒子在平行金属板间的运动轨迹,粒子在电场中运动的侧向总位移应满足:
| d |
| 2 |
| 1 |
| 2 |
| qU0 |
| md |
| T |
| 2 |
(3)画出带电粒子在磁场中的运动轨迹,由几何知识求出最小矩形磁场的长和宽,即可求出磁场的最小面积.
解答:解:(1)因带电微粒在P点速度沿x轴正向,则带电微粒在Q点的水平速度为v0,设速度方向与水平方向的夹角为θ,有:
cosθ=
=
,得θ=60°
在Q点的竖直方向分速度为vy=2v0sinθ=
v0
 从P点到Q点,带电微粒做类平抛运动,则有
从P点到Q点,带电微粒做类平抛运动,则有
=2?(
)?
∴d=
L=v0t=v0?
=v0?
=
(2)由题,画出粒子在平行金属板间的运动轨迹,粒子在电场中运动的侧向总位移满足:
=
?
?(
)2?2n,其中n=1,2,3,…
又L=v0?nT
由以上两式解得:U0=
(n=1,2,3,…)
(3)如图,设最大的矩形磁场的高为L1,宽为L2,画出带电粒子的运动轨迹,如图,则由几何知识可知:
(
-r)?cosθ=r,
∴r=
故L1=r(1+cosθ)=
r,L2=r
所以矩形磁场的最小面积为
S=L1?L2=
r2=
=
答:
(1)平行金属板M、N间的距离d为
,右侧电场的宽度L是
;
(2)平行金属板上所加电压U0满足的条件是:U0=
(n=1,2,3,…);
(3)矩形磁场区域的最小面积是
.
cosθ=
| v0 |
| 2v0 |
| 1 |
| 2 |
在Q点的竖直方向分速度为vy=2v0sinθ=
| 3 |
 从P点到Q点,带电微粒做类平抛运动,则有
从P点到Q点,带电微粒做类平抛运动,则有| v | 2 y |
| qE |
| m |
| d |
| 2 |
∴d=
3m
| ||
| qE |
L=v0t=v0?
| vy |
| a |
| vy | ||
|
| ||||
| qE |
(2)由题,画出粒子在平行金属板间的运动轨迹,粒子在电场中运动的侧向总位移满足:
| d |
| 2 |
| 1 |
| 2 |
| qU0 |
| md |
| T |
| 2 |

又L=v0?nT
由以上两式解得:U0=
6nm
| ||
| q |
(3)如图,设最大的矩形磁场的高为L1,宽为L2,画出带电粒子的运动轨迹,如图,则由几何知识可知:
(
| d |
| 2 |
∴r=
| d |
| 6 |
故L1=r(1+cosθ)=
| 3 |
| 2 |
所以矩形磁场的最小面积为
S=L1?L2=
| 3 |
| 2 |
| d2 |
| 24 |
3m2
| ||
| 8q2E2 |
答:
(1)平行金属板M、N间的距离d为
3m
| ||
| qE |
| ||||
| qE |
(2)平行金属板上所加电压U0满足的条件是:U0=
6nm
| ||
| q |
(3)矩形磁场区域的最小面积是
3m2
| ||
| 8q2E2 |
点评:本题带电粒子在复合场中运动,电场中做平抛运动,关键要把握电场的周期性,磁场中画出粒子运动的轨迹,由几何知识求磁场的长和宽是关键.

练习册系列答案
相关题目

 如图所示的直角坐标系中,在y≥0的区域有一垂直于xoy平面的匀强磁场,在第四象限内有一平行于x轴方向的匀强电场.现使一个质量为m,电荷为+q的带电粒子,从坐标原点O以速度v0沿着y轴力向射入匀强磁场,带电粒子从P(x,0)点射出磁场又从Q(0,-y)点射出匀强电场,射出电场时粒子速度跟y轴夹角120°.(不计粒子重力)求:
如图所示的直角坐标系中,在y≥0的区域有一垂直于xoy平面的匀强磁场,在第四象限内有一平行于x轴方向的匀强电场.现使一个质量为m,电荷为+q的带电粒子,从坐标原点O以速度v0沿着y轴力向射入匀强磁场,带电粒子从P(x,0)点射出磁场又从Q(0,-y)点射出匀强电场,射出电场时粒子速度跟y轴夹角120°.(不计粒子重力)求: 如图所示的直角坐标系xOy中,x<0,y>0的区域内有沿x轴正方向的匀强电场,x≥0的区域内有垂直于xOy坐标平面向外的匀强磁场,x轴上P点坐标为(-L,0),y轴上M点的坐标为(0,
如图所示的直角坐标系xOy中,x<0,y>0的区域内有沿x轴正方向的匀强电场,x≥0的区域内有垂直于xOy坐标平面向外的匀强磁场,x轴上P点坐标为(-L,0),y轴上M点的坐标为(0,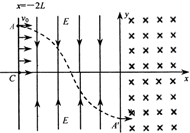 如图所示的直角坐标系中,第Ⅰ、Ⅳ象限内存在着垂直纸面向里的匀强磁场,在x=-2L与y轴之间第Ⅱ、Ⅲ象限内存在大小相等,方向相反的匀强电场,场强方向如图所示.在A(-2L,L)到C(-2L,0)的连线上连续分布着电量为+q、质量为m的粒子.从t=0时刻起,这些带电粒子依次以相同的速度ν沿x轴正方向射出.从A点射入的粒子刚好沿如图所示的运动轨迹从y轴上的A′(0,-L)沿x轴正方向穿过y轴.不计粒子的重力及它们间的相互作用,不考虑粒子间的碰撞.
如图所示的直角坐标系中,第Ⅰ、Ⅳ象限内存在着垂直纸面向里的匀强磁场,在x=-2L与y轴之间第Ⅱ、Ⅲ象限内存在大小相等,方向相反的匀强电场,场强方向如图所示.在A(-2L,L)到C(-2L,0)的连线上连续分布着电量为+q、质量为m的粒子.从t=0时刻起,这些带电粒子依次以相同的速度ν沿x轴正方向射出.从A点射入的粒子刚好沿如图所示的运动轨迹从y轴上的A′(0,-L)沿x轴正方向穿过y轴.不计粒子的重力及它们间的相互作用,不考虑粒子间的碰撞. 空间中有一匀强电场,在电场中建立如图所示的直角坐标系o-xyz,M,N为电场中的两个点.M点坐标为(0,-a,0),N点坐标为(
空间中有一匀强电场,在电场中建立如图所示的直角坐标系o-xyz,M,N为电场中的两个点.M点坐标为(0,-a,0),N点坐标为(