题目内容
12. 如图,Q为一个原来静止在光滑水平面上的物体,其DB段为一半径为R的光滑圆弧轨道,AD段为一长度为L=R的粗糙水平轨道,二者相切于D点,D在圆心O的正下方,整个轨道位于同一竖直平面内.物块P的质量为m(可视为质点),P与AD间的动摩擦因数μ=0.1,物体Q的质量为M=2m,重力加速度为g.
如图,Q为一个原来静止在光滑水平面上的物体,其DB段为一半径为R的光滑圆弧轨道,AD段为一长度为L=R的粗糙水平轨道,二者相切于D点,D在圆心O的正下方,整个轨道位于同一竖直平面内.物块P的质量为m(可视为质点),P与AD间的动摩擦因数μ=0.1,物体Q的质量为M=2m,重力加速度为g.(1)若Q固定,P以速度v0从A点滑上水平轨道,冲至C点后返回A点时恰好静止,求v0大小.
(2)若Q固定,P仍以速度v0从A点滑上水平轨道,求P第一次越过D点时对D点的压力大小.
(3)若Q不固定,P仍以速度v0从A点滑上水平轨道,求P在光滑圆弧轨道上所能达到的最大高度h.
分析 (1、2)P从A到C又返回A的过程中,由动能定理求得v0的大小,由动能定理和牛顿定律求解对Q的压力大小.
(3)当PQ具有共同速度v时,P达到的最大高度h,由动量守恒定律和功能关系求解.
解答 解:(1)P从A到C又返回A的过程中,由动能定理有
-μmg•2L=0-$\frac{1}{2}$m${v}_{0}^{2}$ ①
将L=R代入①解得
v0=$\sqrt{\frac{2gR}{5}}$ ②
(2)若P在D点的速度为vD,Q对P的支持力为FD,由动能定理和牛顿定律有
-μmgL=$\frac{1}{2}$m${v}_{D}^{2}$-$\frac{1}{2}$m${v}_{0}^{2}$ ③
根据牛顿第二定律得
FD-mg=m$\frac{{v}_{D}^{2}}{R}$ ④
联立解得
FD=1.2mg ⑤
由牛顿第三定律可知,P对Q的压力大小也为1.2mg.
(3)当PQ具有共同速度v时,P达到的最大高度h,由动量守恒定律有
mv0=(m+M)v ⑥
由功能关系有$\frac{1}{2}$m${v}_{0}^{2}$=μmgL+$\frac{1}{2}$(m+M)v2+mgh ⑦
联立解得
h=$\frac{1}{30}$R
答:(1)若Q固定,P以速度v0从A点滑上水平轨道,冲至C点后返回A点时恰好静止,v0大小是$\sqrt{\frac{2gR}{5}}$.
(2)若Q固定,P仍以速度v0从A点滑上水平轨道,P第一次越过D点时对D点的压力大小是1.2mg.
(3)若Q不固定,P仍以速度v0从A点滑上水平轨道,P在光滑圆弧轨道上所能达到的最大高度是$\frac{1}{30}$R.
点评 本题主要考查了牛顿第二定律、动量守恒定律及动能定理的直接应用,难度适中.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案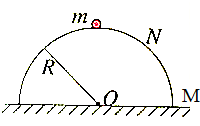 如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )
如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )| A. | 沿球面下滑至最低点M | |
| B. | 沿球面下滑至某一点N,便离开球面做斜下抛运动 | |
| C. | 立即离开球面做平抛运动 | |
| D. | 以上说法都不正确 |
 如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )
如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )| A. | 2s末F做功的功率为0 | B. | 2s内小球的位移为20m | ||
| C. | 第1s内小球的速度变化了10m/s | D. | 第1s内F做功为100J |
| A. | 欧姆流行的“地心说” | |
| B. | 牛顿第二定律 | |
| C. | 牛顿第三定律 | |
| D. | 卡文迪许通过扭秤实验得出的引力常量 |
 如图所示,人重600N,木板重400N,人与木板、木板与地面间的动摩擦因数均为0.2,现在人用水平拉力拉绳,使他与木板一起向右匀速运动,则( )
如图所示,人重600N,木板重400N,人与木板、木板与地面间的动摩擦因数均为0.2,现在人用水平拉力拉绳,使他与木板一起向右匀速运动,则( )| A. | 人拉绳的力是200 N | |
| B. | 人拉绳的力是50 N | |
| C. | 人的脚给木板的摩擦力方向水平向左 | |
| D. | 人的脚给木板的摩擦力方向水平向右 |
| A. | 5s | B. | 1s | C. | 3s | D. | 4s |
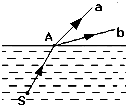
| A. | 在水中a光的速度比b光的速度小 | |
| B. | a光的频率小于b光的频率 | |
| C. | 若a、b两种单色光由玻璃射向空气时,a光的临界角较小 | |
| D. | 若保持入射点A位置不变,将入射光线顺时针旋转,则从水面上方观察,a光先消失 |
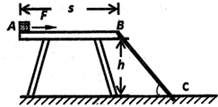 如图所示,小物体质量m=1kg,放在高度为h=5m、长度为S=10m的粗糙水平固定平台的左端A点,小物体与桌面之间的动摩擦因数μ=0.1,在水平平台的右侧有一倾角为53°的斜面BC.现用水平拉力F=3N从静止开始作用于小物体.不计空气阻力.试求:(g取10m/s2)
如图所示,小物体质量m=1kg,放在高度为h=5m、长度为S=10m的粗糙水平固定平台的左端A点,小物体与桌面之间的动摩擦因数μ=0.1,在水平平台的右侧有一倾角为53°的斜面BC.现用水平拉力F=3N从静止开始作用于小物体.不计空气阻力.试求:(g取10m/s2) 2015年新春佳节,我市的许多餐厅生意火爆,常常人满为患,为能服务更多的顾客,服务员需要用最短的时间将菜肴送至顾客处.某次服务员用单手托托盘方式(如图)给10m远处的顾客上菜,要求全程托盘水平且手、托盘和碗之间无相对滑动.已知托盘和手、碗之间的摩擦因数分别为0.2、0.125,服务员上菜最大速度为2.5m/s.假设服务员加速、减速运动过程中是匀变速直线运动,且可认为最大静摩擦力等于滑动摩擦力.则服务员上菜所用的最短时间是多少?
2015年新春佳节,我市的许多餐厅生意火爆,常常人满为患,为能服务更多的顾客,服务员需要用最短的时间将菜肴送至顾客处.某次服务员用单手托托盘方式(如图)给10m远处的顾客上菜,要求全程托盘水平且手、托盘和碗之间无相对滑动.已知托盘和手、碗之间的摩擦因数分别为0.2、0.125,服务员上菜最大速度为2.5m/s.假设服务员加速、减速运动过程中是匀变速直线运动,且可认为最大静摩擦力等于滑动摩擦力.则服务员上菜所用的最短时间是多少?