题目内容
16．
在汽车内的悬线上挂着一个小球m，实验表明当汽车做匀变速直线运动时，悬线将与竖直方向成某一固定角度θ，如图所示．若在汽车底板上还有一个跟它相对静止的物体M，则关于汽车的运动情况和物体M的受力情况分析正确的是（ ）| A． | 汽车一定向右做加速运动 | |
| B． | 汽车一定向左做加速运动 | |
| C． | M除受到重力、底板的支持力作用外，还一定受到向左的摩擦力的作用 | |
| D． | M除受到重力、底板的支持力作用外，还一定受到向右的摩擦力的作用 |
分析 先以小球为研究对象，分析受力情况，根据牛顿第二定律可求得加速度，判断汽车的运动情况；
再以M为研究对象，根据牛顿第二定律，分析受力情况．
解答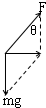 
解：A、B、以小球为研究对象，分析受力情况：重力mg和细线的拉力F，由于小球的加速度水平向右，根据牛顿第二定律得知，小球的合力也水平向右，如图，则有
mgtanθ=ma，得a=gtanθ，θ一定，则加速度a一定，汽车的加速度也一定，则汽车可能向右做匀加速运动，也可能向左做匀减速运动．故AB错误．
C、D对M：M受到重力、底板的支持力．M相对于汽车静止，M的加速度必定水平向右，根据牛顿第二定律得知，一定受到水平向右的摩擦力．故C错误，D正确．
故选：D．
点评 本题运用合成法研究小球的加速度，关键抓住小球的加速度与汽车相同，沿水平向右方向，由牛顿第二定律分析受力情况
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．某振子的固有频率为f0，在周期性驱动力的作用下做受迫振动，驱动力的频率为f．若驱动力的振幅保持不变，下列说法正确的是（ ）
| A． | 当f＜f0时，该振子的振幅随f增大而减小 | |
| B． | 当f＞f0时，该振子的振幅随f减小而增大 | |
| C． | 该振子的振动稳定后，振动的频率等于f0 | |
| D． | 该振子的振动稳定后，振动的频率等于f |
7．
如图所示，固定的倾斜光滑杆上套有一个质量为m的小球，小球与一轻质弹簧一端相连，弹簧的另一端固定在地面上的A点，已知杆与水平面之间的夹角θ＜45°，当小球位于B点时，弹簧与杆垂直，此时弹簧处于原长．现让小球自C点由静止释放，在小球滑到杆底端的整个过程中，关于小球的动能、重力势能和弹簧的弹性势能，下列说法正确的是（ ）
如图所示，固定的倾斜光滑杆上套有一个质量为m的小球，小球与一轻质弹簧一端相连，弹簧的另一端固定在地面上的A点，已知杆与水平面之间的夹角θ＜45°，当小球位于B点时，弹簧与杆垂直，此时弹簧处于原长．现让小球自C点由静止释放，在小球滑到杆底端的整个过程中，关于小球的动能、重力势能和弹簧的弹性势能，下列说法正确的是（ ）| A． | 小球的动能与重力势能之和保持不变 | |
| B． | 小球的动能与重力势能之和先增大后减少 | |
| C． | 小球的动能与弹簧的弹性势能之和先减少后增大 | |
| D． | 小球的重力势能与弹簧的弹性势能之和保持不变 |
一列简谐横波沿x轴正方向传播，t=0时刻的波形如图所示，经0.6s时间质点a从t=0开始第一次到达波峰位置，则这列波的传播速度为5m/s，质点b第一次出现在波谷的时刻为1.4s．
1．一个理想变压器原、副线圈匝数比n1：n2=11：5正弦交变电源连接，输入电压U如图甲所示，如图乙所示副线圈接入一个10Ω的电阻，一个电压表与电阻并联，则（ ）
| A． | 流过电阻的电流是20A | |
| B． | 与电阻并联的电压表的示数是100V | |
| C． | 经过60s电阻发出的热量是1.2×105J | |
| D． | 变压器的输入功率是1×103W |
8．
如图是回旋加速器的示意图，其核心部分是两个半径为R的D形金属盒，两金属盒表面与磁感应强度为B的匀强磁场垂直，并分别与一个高频电源两端相连．现用它来加速质量为m、电荷量为q的微观粒子，则下列说法正确的是（ ）
如图是回旋加速器的示意图，其核心部分是两个半径为R的D形金属盒，两金属盒表面与磁感应强度为B的匀强磁场垂直，并分别与一个高频电源两端相连．现用它来加速质量为m、电荷量为q的微观粒子，则下列说法正确的是（ ）| A． | 要使回旋加速器正常工作，高频电源的频率应为$\frac{qB}{πm}$ | |
| B． | 输出粒子获得的最大动能为$\frac{（qBR）^{2}}{2m}$ | |
| C． | 要提高粒子输出时的最大速度，需提高电源的电压 | |
| D． | 若先后用来加速氘核（${\;}_{1}^{2}$H）和氦核（${\;}_{2}^{4}$He），则必须调整电源的频率 |
5．
一束带电粒子（质量为m）以速度v沿半径方向垂直射入磁感应强度为B，半径为R的圆形匀强磁场区域，离开磁场时速度方向改变了60°，如图所示．则（ ）
一束带电粒子（质量为m）以速度v沿半径方向垂直射入磁感应强度为B，半径为R的圆形匀强磁场区域，离开磁场时速度方向改变了60°，如图所示．则（ ）| A． | 该粒子的比荷$\frac{q}{m}=\frac{{\sqrt{3}v}}{3rB}$ | |
| B． | 穿过磁场的时间为$\frac{πR}{3v}$ | |
| C． | 电子束运动的轨道半径为2R | |
| D． | 若射入的速度增大，电子束的偏转角也会增大 |
