题目内容
如图 所示，光滑水平地面上有一足够长的木板，左端放置可视为质点的物体，其质量为m1=1kg，木板与物体间动摩擦因数μ=0.1．二者以相同的初速度Vo=0.8m/s-起向右运动，木板与竖直墙碰撞时间极短，且没有机械能损失．V=10m/s2．I．如果木板质量m2=3kg，求物体相对木板滑动的最大距离；
II．如果木板质量m2=0.6kg，求物体相对木板滑动的最大距离．
【答案】分析：I．木板与竖直墙碰撞后，以原速反弹，根据动量守恒定律求出两者最终的速度，根据能量守恒定律求出物体相对木板滑动的最大距离．
II．木板与竖直墙碰撞后，以原速反弹，根据动量守恒定律知木板将与竖直墙再次碰撞，最后木板停在竖直墙处，根据能量守恒定律求出物体相对木板滑动的最大距离．
解答：解：Ⅰ．木板与竖直墙碰撞后，以原速反弹，由动量守恒定律
m2v-m1v=（m1+m2）v
v=0.4m/s，方向向左，不会与竖直墙再次碰撞．
由能量守恒定律
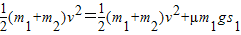
解得 s1=0.96m
Ⅱ．木板与竖直墙碰撞后，以原速反弹，由动量守恒定律
m2v-m1v=（m1+m2）v′
v′=-0.2m/s，方向向右，将与竖直墙再次碰撞，最后木板停在竖直墙处
由能量守恒定律
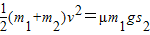
解得 s2=0.512m．
答：（1）如果木板质量m2=3kg，求物体相对木板滑动的最大距离为0.96m．
（2）如果木板质量m2=0.6kg，求物体相对木板滑动的最大距离为0.512m．
点评：本题综合运用了动量守恒定律和能量守恒定律，难度较大，关键是根据动量守恒定律理清木板和木块最终的运动情况．
II．木板与竖直墙碰撞后，以原速反弹，根据动量守恒定律知木板将与竖直墙再次碰撞，最后木板停在竖直墙处，根据能量守恒定律求出物体相对木板滑动的最大距离．
解答：解：Ⅰ．木板与竖直墙碰撞后，以原速反弹，由动量守恒定律
m2v-m1v=（m1+m2）v
v=0.4m/s，方向向左，不会与竖直墙再次碰撞．
由能量守恒定律
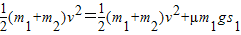
解得 s1=0.96m
Ⅱ．木板与竖直墙碰撞后，以原速反弹，由动量守恒定律
m2v-m1v=（m1+m2）v′
v′=-0.2m/s，方向向右，将与竖直墙再次碰撞，最后木板停在竖直墙处
由能量守恒定律
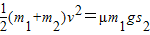
解得 s2=0.512m．
答：（1）如果木板质量m2=3kg，求物体相对木板滑动的最大距离为0.96m．
（2）如果木板质量m2=0.6kg，求物体相对木板滑动的最大距离为0.512m．
点评：本题综合运用了动量守恒定律和能量守恒定律，难度较大，关键是根据动量守恒定律理清木板和木块最终的运动情况．
练习册系列答案
口算能手系列答案
相关题目
（2012?济南一模）如图所示，光滑水平面上放置质量分别为m、2m和3m的三个木块，其中质量为2m和3m的木块间用一轻弹簧相连，轻弹簧能承受的最大拉力为T．现用水平拉力F拉质量为3m的木块，使三个木块一起加速运动，则以下说法正确的是（ ）
如图所示，光滑水平面上有一木板，质量M=1.0kg，长度L=1.0m．在木板的最左端有一个小铁块（可视为质点），质量m=1.0kg．小铁块与木板之间的动摩擦因数μ=0.30．开始时它们都处于静止状态，某时刻起对木板施加一个水平向左的拉力F，g取l0/s2．求：
如图所示，光滑水平面上有辆静止的绝缘小车，车上固定两块竖直带电金属板A、B，A、B间距为d，其间匀强电场的强度为E，方向水平向左，车和A、B的总质量为M，今有一个质量为m、带电量为+q的微粒C，以水平向右的速度v0从金属板B的中心小孔射入电场中，欲使带电微粒C不打到A板上，v0必须满足的条件？
如图所示，光滑水平面上静止放着长L=1.6m，质量为M=3kg的木块（厚度不计），一个质量为m=1kg的小物体放在木板的最右端，m和M之间的动摩擦因数μ=0.1，今对木板施加一水平向右的拉力F，（g取10m/s2）
如图所示，光滑水平面上有正方形金属线框abcd，边长为L、电阻为R、质量为m．虚线PP’和QQ’之间有一竖直向上的匀强磁场，磁感应强度为B，宽度为H，且H＞L．线框在恒力F0作用下由静止开始向磁场区域运动，cd边运动S后进入磁场，ab边进入磁场前某时刻，线框已经达到平衡状态．当cd边到达QQ’时，撤去恒力F0，重新施加外力F，使得线框做加速度大小为F0/m的匀减速运动，最终离开磁场．