题目内容
如果以速度v0 将小球从地面竖直上抛,抛出时计时,那么小球速率变为
时与
时物体距地面的高度比为
.
| v0 |
| 2 |
| v0 |
| 4 |
| 4 |
| 5 |
| 4 |
| 5 |
分析:根据匀变速直线运动位移速度公式列式即可求解.
解答:解:小球以速度v0从地面竖直向上抛出,小球速率变为
有:
2gh=(
)2-v02 ①
当小球以速度v0从地面竖直向上抛出,小球速率变为
有:
2gh′=(
)2-v02 ②
由①②解得:
=
故答案为:
| v0 |
| 2 |
2gh=(
| v0 |
| 2 |
当小球以速度v0从地面竖直向上抛出,小球速率变为
| v0 |
| 4 |
2gh′=(
| v0 |
| 4 |
由①②解得:
| h |
| h′ |
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
点评:本题主要考查了匀变速直线运动位移速度公式的直接应用,难度不大,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
如图所示,一质量为m的小方块(可视为质点),系在一伸直的轻绳一端,绳的另一端固定在粗糙水平面上,绳长为r.给小方块一沿垂直轻绳的初速度v0,质点将在该水平面上以绳长为半径做圆周运动,运动一周后,其速率变为v0/2 ,则以下说法正确的是( )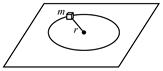
| A.如果初速度v0较小,绳的拉力可能为0 |
| B.绳拉力的大小随物体转过的角度均匀减小 |
C.质点运动一周的时间为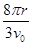 |
D.质点运动一周克服摩擦力做的功为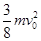 |
如图所示,一质量为m的小方块(可视为质点),系在一伸直的轻绳一端,绳的另一端固定在粗糙水平面上,绳长为r.给小方块一沿垂直轻绳的初速度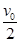 v0,质点将在该水平面上以绳长为半径做圆周运动,运动一周后,其速率变为 ,则以下说法正确的是
v0,质点将在该水平面上以绳长为半径做圆周运动,运动一周后,其速率变为 ,则以下说法正确的是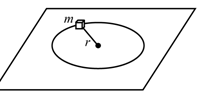
| A.如果初速度v0较小,绳的拉力可能为0 |
| B.绳拉力的大小随物体转过的角度均匀减小 |
C.质点运动一周的时间为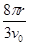 |
D.质点运动一周克服摩擦力做的功为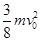 |
 如图所示,一质量为m的小方块(可视为质点)系在一伸直的轻绳一端,绳的另一端固定在粗糙水平面上,绳长为r.给小方块一沿垂直轻绳的初速度v0,质点将在该水平面上以绳长为半径做圆周运动,运动一周后,其速率变为
如图所示,一质量为m的小方块(可视为质点)系在一伸直的轻绳一端,绳的另一端固定在粗糙水平面上,绳长为r.给小方块一沿垂直轻绳的初速度v0,质点将在该水平面上以绳长为半径做圆周运动,运动一周后,其速率变为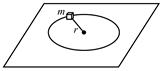
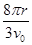
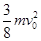
 v0,质点将在该水平面上以绳长为半径做圆周运动,运动一周后,其速率变为 ,则以下说法正确的是
v0,质点将在该水平面上以绳长为半径做圆周运动,运动一周后,其速率变为 ,则以下说法正确的是

