Question

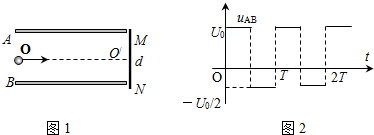
长为L的平行金属板，板间形成匀强电场，一个带电为+q、质量为m的带电粒子（不计重力），以初速度v₀紧贴上板沿垂直于电场线方向射入匀强电场．刚好从下板边缘射出，末速度恰与下板成45°，如图所示，求：
（1）粒子末速度的大小；
（2）两板间的距离d；
（3）匀强电场电场强度的大小．

Answer 1

分析：（1）粒子在电场中做类平抛运动，由运动的合成与分解可知粒子的末速度的大小；
（2）根据粒子在水平方向和竖直方向上的运动规律，结合等时性，运用运动学公式求出两板间的距离d．
（3）将粒子的运动分解为水平方向的匀速运动和竖直方向的匀加速直线运动，则由运动的合成与分解可求得电场强度；

解答：解：（1）根据平行四边形定则得，粒子的末速度v=

v0

cos45°

=

2

v0．
（2）粒子出磁场时在竖直方向上的分速度v_y=v₀
则水平方向上有L=v₀t，
解得t=

L

v0

则两板间的距离d=

vy

2

t=

v0

2

×

L

v0

=

L

2

．
（3）根据d=

1

2

at2，a=

qE

m

得，
解得E=

mv02

qL

．
答：（1）粒子的末速度大小为

2

v0．
（2）两板间的距离为

L

2

．
（3）匀强电场的电场强度大小为

mv02

qL

．

点评：带电粒子在电场中的运动，若垂直电场线进入，则做类平抛运动，要将运动分解为沿电场线和垂直于电场线两个方向进行分析，利用直线运动的规律进行求解．