题目内容
 在某市区内,一辆小汽车在平直公路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路,汽车司机发现前方有危险(游客正在D处向北走)经0.7s作出反应,从A点开始紧急刹车,但仍将正步行至B处的游客撞伤,该汽车最终在C处停下.为了清晰了解事故现场,现以如图示之:
在某市区内,一辆小汽车在平直公路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路,汽车司机发现前方有危险(游客正在D处向北走)经0.7s作出反应,从A点开始紧急刹车,但仍将正步行至B处的游客撞伤,该汽车最终在C处停下.为了清晰了解事故现场,现以如图示之:为了判断汽车司机是否超速行驶,并测出肇事汽车速度vA,警方派一车胎磨损情况与肇事车相当的车以法定最高速度vm=14.0m/s行驶在同一马路的同一地段,在肇事汽车的出事点B急刹车,恰好也在C点停下来.在事故现场测得AB=17.5m、BC=14.0m、BD=2.6m,问:
(1)该肇事汽车的初速度vA是多大?
(2)游客横过马路的速度是多大?
分析:因为警车从B点刹车,初末速度已知,位移已知,可以由位移速度关系式解得加速度,然后肇事车从A点刹车到C点停止,末速度、位移、加速度都是已知,再由位移速度关系式解出肇事车的初速度.
解答:解:(1)以警车为研究对象,研究从B到C的刹车过程,
则:v2-v02=-2ax
将v0=14.0m/s,x=14.0m,v=0代入
解得警车刹车加速度大小为:a=7.0m/s2,
因为警车行驶条件与肇事汽车相同,则肇事汽车的加速度a′=a=7.0m/s2.
对于肇事汽车从A到C的刹车过程,有:0-vA2=-2axAC
所以肇事汽车的初速度vA=
=
m/s=21m/s
(2)肇事汽车在出事点B的速度:
VB=
=14m/s
肇事汽车通过sAB段的平均速度:
=
=
m/s=17.5m/s
肇事汽车通过sAB段的时间:
t2=
=
s=1s
所以游客横过马路的速度:vD=
=
m/s=1.53m/s
答:肇事汽车的初速度vA是21m/s,游客横过马路的速度是1.53m/s
则:v2-v02=-2ax
将v0=14.0m/s,x=14.0m,v=0代入
解得警车刹车加速度大小为:a=7.0m/s2,
因为警车行驶条件与肇事汽车相同,则肇事汽车的加速度a′=a=7.0m/s2.
对于肇事汽车从A到C的刹车过程,有:0-vA2=-2axAC
所以肇事汽车的初速度vA=
| 2axAC |
| 2×7×(17.5+14) |
(2)肇事汽车在出事点B的速度:
VB=
| 2a′xBC |
肇事汽车通过sAB段的平均速度:
. |
| v |
| vA+vB |
| 2 |
| 21+14 |
| 2 |
肇事汽车通过sAB段的时间:
t2=
| sAB | ||
|
| 17.5 |
| 17.5 |
所以游客横过马路的速度:vD=
| sBD |
| t1+t2 |
| 2.6 |
| 0.7+1 |
答:肇事汽车的初速度vA是21m/s,游客横过马路的速度是1.53m/s
点评:在解决物理问题时,有时语言描述不好懂,我们可以结合图象更清晰直观的理解题目.

练习册系列答案
相关题目
 如图所示,在某市区内,一辆小汽车在公路上以速度v1向东行驶,一位观光游客由南向北从斑马线上横穿马路.汽车司机发现游客途经D处时经过0.7s做出反应紧急刹车,但仍将正步行至B处的游客撞伤,该汽车最终在C处停下.为了判断汽车是否超速行驶以及游客横穿马路是否过快,警方派一警车以法定最高速度vm=14.Om/s行驶在同一马路的同一地段,在肇事汽车的起始制动点A紧急刹车,经过14.Om后停下来.在事故现场测量得xAB=17.5m、xBC=14.Om、XBD=2.6m.肇事汽车刹车性能良好(可认为警车与肇事汽车刹车时加速度均相同).问:
如图所示,在某市区内,一辆小汽车在公路上以速度v1向东行驶,一位观光游客由南向北从斑马线上横穿马路.汽车司机发现游客途经D处时经过0.7s做出反应紧急刹车,但仍将正步行至B处的游客撞伤,该汽车最终在C处停下.为了判断汽车是否超速行驶以及游客横穿马路是否过快,警方派一警车以法定最高速度vm=14.Om/s行驶在同一马路的同一地段,在肇事汽车的起始制动点A紧急刹车,经过14.Om后停下来.在事故现场测量得xAB=17.5m、xBC=14.Om、XBD=2.6m.肇事汽车刹车性能良好(可认为警车与肇事汽车刹车时加速度均相同).问: 在某市区内,一辆小汽车在平直的公路上以速度v向东匀速行驶,一位观光游客正由南向北从斑马线上匀速横穿马路.汽车司机发现前方有危险(游客正在D处)经0.3s作出反应,紧急刹车,但仍将正步行至B处的游客撞伤,该汽车最终在C处停下,为了清晰了解事故现场,现以下图示之,AC段是汽车轮胎在路面上的擦痕.为了判断汽车司机是否超速行驶,警方派一警车以该路段法定最高速度vm=14.0m/s行驶在同一马路的同一地段,在肇事汽车起始制动点A紧急刹车,经14.0m后停下来,在事故现场测得AB=17.5m.BC=14.0m,BD=2.6m.问:
在某市区内,一辆小汽车在平直的公路上以速度v向东匀速行驶,一位观光游客正由南向北从斑马线上匀速横穿马路.汽车司机发现前方有危险(游客正在D处)经0.3s作出反应,紧急刹车,但仍将正步行至B处的游客撞伤,该汽车最终在C处停下,为了清晰了解事故现场,现以下图示之,AC段是汽车轮胎在路面上的擦痕.为了判断汽车司机是否超速行驶,警方派一警车以该路段法定最高速度vm=14.0m/s行驶在同一马路的同一地段,在肇事汽车起始制动点A紧急刹车,经14.0m后停下来,在事故现场测得AB=17.5m.BC=14.0m,BD=2.6m.问: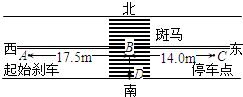 在某市区内,一辆小汽车在平直公路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路,汽车司机发现前方有危险(游客正在D处向北走)经0.7s作出反应,从A点开始紧急刹车,但仍将正步行至B处的游客撞伤,该汽车最终在C处停下.为了清晰了解事故现场,现以下图示之:为了判断汽车司机是否超速行驶,并测出肇事汽车速度vA,警方派一车胎磨损情况与肇事车相当的车以法定最高速度vm=14m/s行驶在同一马路的同一地段,在肇事汽车的出事点B急刹车,恰好也在C点停下来.在事故现场测得AB=17.5m、BC=14.0m、BD=3.4m,问:
在某市区内,一辆小汽车在平直公路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路,汽车司机发现前方有危险(游客正在D处向北走)经0.7s作出反应,从A点开始紧急刹车,但仍将正步行至B处的游客撞伤,该汽车最终在C处停下.为了清晰了解事故现场,现以下图示之:为了判断汽车司机是否超速行驶,并测出肇事汽车速度vA,警方派一车胎磨损情况与肇事车相当的车以法定最高速度vm=14m/s行驶在同一马路的同一地段,在肇事汽车的出事点B急刹车,恰好也在C点停下来.在事故现场测得AB=17.5m、BC=14.0m、BD=3.4m,问: 在某市区内,一辆小汽车在平直的公路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上匀速的横过马路,汽车司机发现前方有危险(游客正在D处),经过0.7s 作出反应,在起始制动点A处紧急刹车,但仍将正步行至B处的游客撞伤,并最终在C处停下(A、B、C三点正处在一条直线上).为了清晰了解事故现场,现以图8示之.为了判断汽车司机是否超速行驶,警方派一警车以法定最高速度Vm=14m/s行驶在同一马路的同一地点,也在肇事汽车的起始制动点A紧急刹车,经历14m后停下来,在事故现场测得AB=17.5m,BC=14.0m BD=2.6m,若肇事汽车刹车性能良好,警车与肇事汽车刹车时的加速度相同(取g=10m/s2),问:
在某市区内,一辆小汽车在平直的公路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上匀速的横过马路,汽车司机发现前方有危险(游客正在D处),经过0.7s 作出反应,在起始制动点A处紧急刹车,但仍将正步行至B处的游客撞伤,并最终在C处停下(A、B、C三点正处在一条直线上).为了清晰了解事故现场,现以图8示之.为了判断汽车司机是否超速行驶,警方派一警车以法定最高速度Vm=14m/s行驶在同一马路的同一地点,也在肇事汽车的起始制动点A紧急刹车,经历14m后停下来,在事故现场测得AB=17.5m,BC=14.0m BD=2.6m,若肇事汽车刹车性能良好,警车与肇事汽车刹车时的加速度相同(取g=10m/s2),问: