题目内容
12. 如图所示,在xOy平面直角坐标系中,第一象限内存在着磁感应强度为B,方向垂直纸面向里的匀强磁场,第二象限内存在沿y轴负方向的匀强电场.从x轴上坐标为(L,0)的点M,沿xOy平面向第一象限内同时发射若干个质量均为m、电荷量均为+q的同种粒子.粒子速度大小不等,方向与x轴正方向成45°~135°.粒子经过磁场偏转后都垂直射到y轴上,然后进入第二象限,粒子重力不计.求:
如图所示,在xOy平面直角坐标系中,第一象限内存在着磁感应强度为B,方向垂直纸面向里的匀强磁场,第二象限内存在沿y轴负方向的匀强电场.从x轴上坐标为(L,0)的点M,沿xOy平面向第一象限内同时发射若干个质量均为m、电荷量均为+q的同种粒子.粒子速度大小不等,方向与x轴正方向成45°~135°.粒子经过磁场偏转后都垂直射到y轴上,然后进入第二象限,粒子重力不计.求:(1)y轴上有粒子穿过的区间长度;
(2)最先与最后穿过y轴的粒子的时间间隔;
(3)若发射速度最小的粒子再次回到x轴时的速度大小恰好等于发射速度最大的粒子的发射速度,匀强电场的场强多大?
分析 (1)粒子在磁场中做匀速圆周运动,确定圆心,定出半径,画出运动轨迹,由几何知识求出轨迹半径,并得到y轴上有粒子穿过的区间长度.
(2)根据轨迹的圆心角求出粒子在磁场中运动的时间,即可求得时间间隔.
(3)粒子进入电场做类平抛运动,由动能定理和半径公式结合求解电场强度.
解答 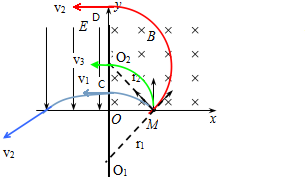 解:(1)画出速度最大的粒子运动轨迹,分别如图中蓝线和红线所示,设它们的半径分别为r1和r2.
解:(1)画出速度最大的粒子运动轨迹,分别如图中蓝线和红线所示,设它们的半径分别为r1和r2.
根据几何知识得:r1=r2=$\sqrt{2}$L
粒子射到y轴上离O最远的点为D,则OD=r2+L=($\sqrt{2}$+1)L
粒子射到y轴上离O最近的点为C,则OC=r1-L=($\sqrt{2}$-1)L
故y轴上有粒子穿过的区间长度为 S=OD-OC=2L.
(2)粒子在磁场中运动的周期为 T=$\frac{2πm}{qB}$
从C射到电场的粒子最先穿过y轴,它在磁场中运动时间为 t1=$\frac{45°}{360°}$T
从D射到电场的粒子最后穿过y轴,它在磁场中运动时间为 t2=$\frac{135°}{360°}$T
故 t2-t1=$\frac{90°}{360°}$T=$\frac{πm}{2qB}$
(3)在速度最小的粒子在电场中做类平抛运动,轨迹如绿线所示,可得其轨迹半径为r3=L
根据r=$\frac{mv}{qB}$,得最大速度为 v1=$\frac{\sqrt{2}qBL}{m}$
最小速度为 v3=$\frac{qBL}{m}$
据题:该粒子再次回到x轴时的速度大小恰好等于发射速度最大的粒子的发射速度,由动能定理有:
qE•L=$\frac{1}{2}m{v}_{1}^{2}$-$\frac{1}{2}m{v}_{3}^{2}$
解得 E=$\frac{q{B}^{2}L}{2m}$
答:
(1)y轴上有粒子穿过的区间长度为2L;
(2)最先与最后穿过y轴的粒子的时间间隔为$\frac{πm}{2qB}$;
(3)若发射速度最小的粒子再次回到x轴时的速度大小恰好等于发射速度最大的粒子的发射速度,匀强电场的场强为$\frac{q{B}^{2}L}{2m}$.
点评 本题的解题关键是通过定圆心,找半径,画出带电粒子的运动轨迹,并运用几何知识求解相关的长度.

| A. | 物体吸热,内能一定增加 | |
| B. | 布朗运动指的是分子的热运动 | |
| C. | 气体的压强是由于大量分子频繁撞击器壁产生的 | |
| D. | 根据油膜实验可知分子在永不停息地做无规则运动 |
| A. | 气体分子的体积是指每个气体分子平均所占有的空间体积 | |
| B. | 晶体外形规则是晶体内部微粒有规则排列的结果 | |
| C. | 在完全失重的情况下,气体对容器壁的压强为零 | |
| D. | 空气中所含水蒸气的压强与同一温度下水的饱和汽压之比称为空气的相对湿度 |
| A. | 探究力的平行四边形定则的实验中采用了理想模型法 | |
| B. | 卡文迪许测定引力常量G的数值时采用了微小量放大的方法 | |
| C. | 伽利略在利用理想实验探究力和运动关系时采用了等效替代法 | |
| D. | 法拉第利用电场线描绘电场是采用了归纳法 |
| A. | 月球的半径 | |
| B. | 月球绕地球做匀速圆周运动的向心加速度 | |
| C. | 月球表面的重力加速度 | |
| D. | 月球的质量 |
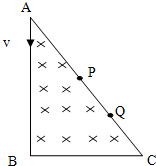 如图所示,直角三角形ABC区域中存在一匀强磁场,比荷相同的两个粒子(不计重力)沿AB方向射入磁场,分别从AC边上的P、Q两点射出,则( )
如图所示,直角三角形ABC区域中存在一匀强磁场,比荷相同的两个粒子(不计重力)沿AB方向射入磁场,分别从AC边上的P、Q两点射出,则( )| A. | 从P点射出的粒子速度大 | |
| B. | 从Q点射出的粒子速度大 | |
| C. | 从Q点射出的粒子在磁场中运动的时间长 | |
| D. | 两个粒子在磁场中运动的时间一样长 |