题目内容
2. 将一质量为1kg的物体以一定的初速度竖直向上抛出,假设物体在运动过程中所受空气阻力的大小恒定不变,其速度-时间图象如图所示,取g=10m/s2,求:
将一质量为1kg的物体以一定的初速度竖直向上抛出,假设物体在运动过程中所受空气阻力的大小恒定不变,其速度-时间图象如图所示,取g=10m/s2,求:(1)物体受到的阻力大小.
(2)图中坐标x的值.
(3)物体落到抛出点时的时间.
分析 (1)根据速度时间图线的斜率求出得出上升时物体的加速度大小,根据牛顿第二定律求出阻力的大小;
(2)根据牛顿第二定律求出下降的加速度,结合速度公式即可求出x的值.
(3)先根据位移公式求出下落的时间,上升与下落的时间的和即为所求.
解答 解:(1)物体向上做匀减速运动的加速度大小 a1=$\frac{△{v}_{1}}{{t}_{1}}$=$\frac{22}{1}$=11m/s2,
根据牛顿第二定律得,mg+f=ma1,
解得阻力:f=ma1-mg=1×11-1×10=1N.
(2)物体下落过程有:mg-f=ma2,
代入数据得:a2=9m/s2,
物体下落的时间:t2=3-2=1s
所以末速度的大小:v′=a2t2=9×1=9m/s
由于下落时速度的方向向下,与初速度的方向相反,所以x的位置是-9m/s,即x的值是9;
(3)由图象可得,当物体回到抛出点,上升的位移大小与下降的位移大小相等,则有:
$\frac{1}{2}{a}_{2}{t}_{3}^{2}=\frac{{v}_{0}}{2}×{t}_{1}$
即:$\frac{1}{2}$×2×22=$\frac{1}{2}$×9×t32
解得下降过程的运动时间t=$\frac{2}{3}\sqrt{11}$s
则物体落回到抛出点的时间为(2+$\frac{2}{3}\sqrt{11}$)s
答:(1)物体受到的阻力大小是1N.
(2)图中坐标x的值是9.
(3)物体落到抛出点时的时间是(2+$\frac{2}{3}\sqrt{11}$)s.
点评 本题考查了牛顿第二定律和速度时间图线的运用,知道加速度是联系力学和运动学的桥梁,知道图线的斜率表示加速度,图线与时间轴围成的面积表示位移.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
8. 2013年修订版《机动车驾驶证申领和使用规定》于2013年1月1日正式施行,司机闯黄灯要扣6分,被称为“史上最严交规”.某小轿车驾驶员看到绿灯开始闪时,经短暂思考后开始刹车,小轿车在黄灯刚亮时恰停在停车线上,如图所示.若绿灯开始闪烁时小轿车距停车线距离L=10.5m,则( )
2013年修订版《机动车驾驶证申领和使用规定》于2013年1月1日正式施行,司机闯黄灯要扣6分,被称为“史上最严交规”.某小轿车驾驶员看到绿灯开始闪时,经短暂思考后开始刹车,小轿车在黄灯刚亮时恰停在停车线上,如图所示.若绿灯开始闪烁时小轿车距停车线距离L=10.5m,则( )
 2013年修订版《机动车驾驶证申领和使用规定》于2013年1月1日正式施行,司机闯黄灯要扣6分,被称为“史上最严交规”.某小轿车驾驶员看到绿灯开始闪时,经短暂思考后开始刹车,小轿车在黄灯刚亮时恰停在停车线上,如图所示.若绿灯开始闪烁时小轿车距停车线距离L=10.5m,则( )
2013年修订版《机动车驾驶证申领和使用规定》于2013年1月1日正式施行,司机闯黄灯要扣6分,被称为“史上最严交规”.某小轿车驾驶员看到绿灯开始闪时,经短暂思考后开始刹车,小轿车在黄灯刚亮时恰停在停车线上,如图所示.若绿灯开始闪烁时小轿车距停车线距离L=10.5m,则( )| A. | 小轿车的刹车距离为8m | |
| B. | 小轿车刹车的加速度大小为2.4m/s2 | |
| C. | 绿灯开始闪烁到黄灯刚亮的时间t0为3 s | |
| D. | 绿灯开始闪烁到黄灯刚亮的时间t0为2.5 s |
13.一列简谐波在均匀弹性介质中沿x轴正方向传播,在某一时刻的波形如图所示( )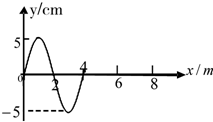

| A. | 当波传到6处时,质点6作简谐运动,但振幅小于5cm | |
| B. | 当波传到6处时,质点2的振动方向向上 | |
| C. | 各质点的振动频率均不一样 | |
| D. | 当质点2振动80次时,质点6振动79次 |
10. 在粗糙程度相同的水平地面上,物块在水平向右的力F作用下由静止开始运动.运动的速度v与时间t的关系如图2所示,取g=10m/s2,由图象可知( )
在粗糙程度相同的水平地面上,物块在水平向右的力F作用下由静止开始运动.运动的速度v与时间t的关系如图2所示,取g=10m/s2,由图象可知( )
 在粗糙程度相同的水平地面上,物块在水平向右的力F作用下由静止开始运动.运动的速度v与时间t的关系如图2所示,取g=10m/s2,由图象可知( )
在粗糙程度相同的水平地面上,物块在水平向右的力F作用下由静止开始运动.运动的速度v与时间t的关系如图2所示,取g=10m/s2,由图象可知( )| A. | 在2s~4s内,力F=0 | B. | 在0~2s内,力F逐渐变小 | ||
| C. | 物块与地面间的动摩擦因数μ=0.2 | D. | 0-6s内物块运动的总位移为16m |
17. A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一变力的作用,该力与时间的关系如图2所示,A、B始终相对静止,则在0~2t0时间内,下列说法不正确的是( )
A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一变力的作用,该力与时间的关系如图2所示,A、B始终相对静止,则在0~2t0时间内,下列说法不正确的是( )
 A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一变力的作用,该力与时间的关系如图2所示,A、B始终相对静止,则在0~2t0时间内,下列说法不正确的是( )
A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一变力的作用,该力与时间的关系如图2所示,A、B始终相对静止,则在0~2t0时间内,下列说法不正确的是( )| A. | t0时刻,A、B间静摩擦力最大 | B. | t0时刻,A、B速度最大 | ||
| C. | 2t0时刻,A、B速度最小 | D. | 2t0时刻,A、B位移最大 |
7. 如图所示,足够长的U型光滑金属导轨平面与水平面成某一角度θ(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒ab在这一过程中下滑的位移大小为( )
如图所示,足够长的U型光滑金属导轨平面与水平面成某一角度θ(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒ab在这一过程中下滑的位移大小为( )
 如图所示,足够长的U型光滑金属导轨平面与水平面成某一角度θ(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒ab在这一过程中下滑的位移大小为( )
如图所示,足够长的U型光滑金属导轨平面与水平面成某一角度θ(0<θ<90°),其中MN和PQ平行且间距为L,导轨平面与磁感应强度为B的匀强磁场垂直,导轨电阻不计.金属棒ab由静止开始沿导轨下滑,并与两导轨始终保持垂直且良好接触,ab棒接入电路的电阻为R,当流过ab棒某一横截面的电荷量为q时,金属棒ab在这一过程中下滑的位移大小为( )| A. | $\frac{qR}{4BL}$ | B. | $\frac{qR}{2BL}$ | C. | $\frac{qR}{BL}$ | D. | $\frac{2qR}{BL}$ |
14.一根粗细均匀的铜棒的质量为m,平放在光滑的水平面上,在铜棒轴线方向受水平向右的拉力F做匀加速直线运动,则棒中自左向右各截面处的弹力大小( )
| A. | 都等于F | B. | 逐渐增大 | C. | 逐渐减小 | D. | 都等于零 |
11. 物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )
物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )
 物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )
物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F分别拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则( )| A. | μA>μB,mA<mB | B. | μA<μB,mA<mB | C. | μA>μB,mA>mB | D. | μA<μB,mA>mB |
 如图所示,用长为L=10cm的绝缘细线拴住一个质量为m=0.1kg,带电量为q=$\sqrt{3}×{10^{-2}}$C的小球,线的另一端拴在水平向右的匀强电场中,开始时把小球、线拉到和O在同一水平面上的A点(线拉直),让小球由静止开始释放,当摆线摆到与水平方向成60°角且到达B点时,小球的速度正好为零.g取10m/s2.求:(结果保留一位有效数字)
如图所示,用长为L=10cm的绝缘细线拴住一个质量为m=0.1kg,带电量为q=$\sqrt{3}×{10^{-2}}$C的小球,线的另一端拴在水平向右的匀强电场中,开始时把小球、线拉到和O在同一水平面上的A点(线拉直),让小球由静止开始释放,当摆线摆到与水平方向成60°角且到达B点时,小球的速度正好为零.g取10m/s2.求:(结果保留一位有效数字)