题目内容
1.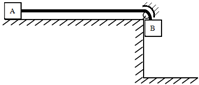 如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求:
如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求:(1)刚释放B物体时,AB物体的加速度为多少?
(2)当B即将落地的瞬间,AB两物体的速度为多少?
(3)在A物体滑到定滑轮前过程中,试写出其加速度与其运动位移的函数关系式,并且作出相应的a-x图象.
分析 (1)对AB及绳沿绳子的方向进行分析,开始下落时,沿绳子的拉力为B的重力,沿绳子由牛顿第二定律列式求解即可;
(2)B即将落地时,B及绳子的重力势能减小,由机械能守恒可求得AB两物体的速度;
(3)整体运动后,平台下方的绳子长度增长,则沿绳子方向上的拉力增大,分析x与台下绳长的关系,结合牛顿第二定律可求得加速度与位移之间的关系.
解答 解:
(1)刚释放瞬间,对B,根据牛顿第二定律,有:mg-T=ma,
对A和软绳整体,根据牛顿第二定律,有:T=2ma
联立以上两式,得:$a=\frac{g}{3}$
(2)B向下运动过程,系统满足机械能守恒,根据系统机械能守恒定律有:$mgL+\frac{1}{2}mg×\frac{L}{2}=\frac{3}{2}m{v}^{2}$
解得:v=$\sqrt{\frac{5}{6}gL}$
(3)对B未落地前,设A运动x距离,对整体据牛顿第二定律,有:$mg+\frac{mg}{2L}x=3ma$
解得:$a=\frac{g}{3}+\frac{gx}{6L}$(x<L)
当x=L时,$a=\frac{g}{2}$,落地后瞬间,B的重力不再产生拉力,此时加速度发生突变,$\frac{mg}{2}=2ma$
则a=$\frac{g}{4}$,即加速度a在物体B落地前后瞬间由$\frac{1}{2}$g变为$\frac{1}{4}$g,
对B落地后,对整体据牛顿第二定律,有:$\frac{mg}{2}=(\frac{m}{2L}(2L-x)+m)a$
解得:a=$\frac{L}{5L-x}g$(x≥L)
答:(1)刚释放B物体时,A、B物体的加速度为$\frac{g}{3}$;
(2)当B即将落地瞬间,A、B两物体的速度为$\sqrt{\frac{5}{6}gL}$;
(3)在A物体滑到定滑轮前过程中,试写出其加速度与运动位移的函数关系式.当x≤L时;a=$a=\frac{g}{3}+\frac{gx}{6L}$;当x>L时,$\frac{L}{5L-x}g$.
点评 本题考查机械能守恒定律及牛顿第二定律的应用,注意本题适用牛顿第二定律中的连接体问题,难点在于绳子的质量不能忽略;故沿绳子方向上的拉力在变化.

 如图所示,两根刚性轻杆上端由自由旋转轴A连接,轻杆下端固定一根自然伸长的匀质轻弹簧,围成边长为L的等边三角形ABC,将此装置竖直放在光滑水平面上,在轴A处施加竖直向下的大小为F的作用力,弹簧被拉伸一定长度,若此时弹簧弹力大小恰为$\frac{F}{2}$,则弹簧的劲度系数为( )
如图所示,两根刚性轻杆上端由自由旋转轴A连接,轻杆下端固定一根自然伸长的匀质轻弹簧,围成边长为L的等边三角形ABC,将此装置竖直放在光滑水平面上,在轴A处施加竖直向下的大小为F的作用力,弹簧被拉伸一定长度,若此时弹簧弹力大小恰为$\frac{F}{2}$,则弹簧的劲度系数为( )| A. | $\frac{F}{(\sqrt{2}-1)L}$ | B. | $\frac{F}{2(\sqrt{2}-1)L}$ | C. | $\frac{F}{(\sqrt{5}-1)L}$ | D. | $\frac{F}{2(\sqrt{5}-1)L}$ |

| A. | 汽车的长度 | B. | 5.0s末汽车牵引力的功率 | ||
| C. | 5.0s内合外力对汽车所做的功 | D. | 5.0s末汽车的速度 |

| A. | 电场力做正功 | B. | 粒子带正电 | C. | 电势能增加 | D. | 加速度减小 |
 质量和带电量都相同的两个粒子,以不同的速率垂直于磁感线方向射入匀强磁场中,两粒子的运动轨迹如图中①、②所示,粒子的重力不计,下列对两个粒子的运动速率υ和在磁场中运动时间t及运动周期T、角速度的说法中正确的是( )
质量和带电量都相同的两个粒子,以不同的速率垂直于磁感线方向射入匀强磁场中,两粒子的运动轨迹如图中①、②所示,粒子的重力不计,下列对两个粒子的运动速率υ和在磁场中运动时间t及运动周期T、角速度的说法中正确的是( )| A. | υ1<υ2 | B. | t1<t2 | C. | T1>T2 | D. | ω1=ω2 |
 如图所示,固定在水平地面上的光滑长直导轨槽,(图为俯视图,图中两组平行双直线表示槽的两侧壁).槽内放置一个滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,滑块的宽度为2R,恰与槽的两内侧壁的间距相等,滑块可在槽内沿槽壁自由滑动.现有一金属小球(可视为质点)以水平初速度v0沿槽的一侧壁冲向滑块,从滑块的半圆形槽口边缘进入滑块凹槽.已知金属小球的质量为m,滑块的质量为3m,整个运动过程中无机械能损失.求:
如图所示,固定在水平地面上的光滑长直导轨槽,(图为俯视图,图中两组平行双直线表示槽的两侧壁).槽内放置一个滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,滑块的宽度为2R,恰与槽的两内侧壁的间距相等,滑块可在槽内沿槽壁自由滑动.现有一金属小球(可视为质点)以水平初速度v0沿槽的一侧壁冲向滑块,从滑块的半圆形槽口边缘进入滑块凹槽.已知金属小球的质量为m,滑块的质量为3m,整个运动过程中无机械能损失.求:
 如图所示,两个倾角均为30°的斜面在O点平滑对接.现将一小球a从A点静止释放,A点距水平地面高d=1.25m.释放a球的同时,另一小球b从O点正上方的B点静止开始下落,b恰能击中a球.(g=10m/s2),求:
如图所示,两个倾角均为30°的斜面在O点平滑对接.现将一小球a从A点静止释放,A点距水平地面高d=1.25m.释放a球的同时,另一小球b从O点正上方的B点静止开始下落,b恰能击中a球.(g=10m/s2),求: 质量为m=2.0kg的物体,从竖直平面内高h=0.45m的光滑弧形轨道上的A点,无初速地沿轨道滑下,并进入水平轨道BC,如图所示.已知物体与水平轨道间的动摩擦因数μ=0.40,求:
质量为m=2.0kg的物体,从竖直平面内高h=0.45m的光滑弧形轨道上的A点,无初速地沿轨道滑下,并进入水平轨道BC,如图所示.已知物体与水平轨道间的动摩擦因数μ=0.40,求: