题目内容
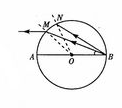
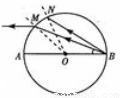
如图所示,一玻璃球体的半径为R,O为球心,AB为直径.来自B点的光线BM在M点射出,出射光线平行于AB,另一光线BN恰好在N点发生全反射.已知∠ABM=30°,求①玻璃的折射率.
②球心O到BN的距离.
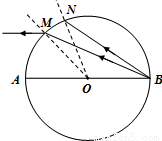
【答案】分析:①根据几何关系找出光线BM的入射角和反射角,利用折射定律可求出玻璃体的折射率.
②根据几何关系求出临界角的正弦值,便可求出球心O到BN的距离.
解答:解:①已知∠ABM=30°,由几何关系知入射角i=∠BMO=30°,折射角β=60°由n=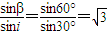
②由题意知临界角C=∠ONB,sinC=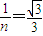 ,则球心O到BN的距离d=RsinC=
,则球心O到BN的距离d=RsinC=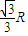 .
.
答:①玻璃的折射率为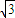 .
.
②球心O到BN的距离为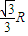 .
.
点评:该题考察了折射定律得应用,要求要熟练的记住折射定律的内容,求折射率时,一定要分清是从介质射向空气还是由空气射入介质;再者就是会用sinC=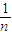 来解决相关问题.
来解决相关问题.
②根据几何关系求出临界角的正弦值,便可求出球心O到BN的距离.
解答:解:①已知∠ABM=30°,由几何关系知入射角i=∠BMO=30°,折射角β=60°由n=
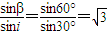
②由题意知临界角C=∠ONB,sinC=
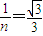 ,则球心O到BN的距离d=RsinC=
,则球心O到BN的距离d=RsinC=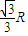 .
.答:①玻璃的折射率为
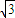 .
.②球心O到BN的距离为
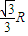 .
.点评:该题考察了折射定律得应用,要求要熟练的记住折射定律的内容,求折射率时,一定要分清是从介质射向空气还是由空气射入介质;再者就是会用sinC=
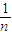 来解决相关问题.
来解决相关问题. 
练习册系列答案
相关题目
 如图所示,一玻璃球体的半径为R,O为球心,AB为直径.来自B点的光线BM在M点射出,出射光线平行于AB,另一光线BN恰好在N点发生全反射.已知∠ABM=30°,求
如图所示,一玻璃球体的半径为R,O为球心,AB为直径.来自B点的光线BM在M点射出,出射光线平行于AB,另一光线BN恰好在N点发生全反射.已知∠ABM=30°,求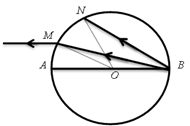
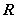
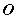
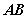
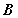
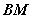
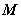
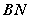
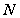
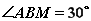
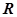 ,
, 为球心,
为球心, 为直径。来自
为直径。来自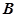 点的光线
点的光线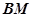 在
在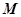 点射出。出射光线平行于
点射出。出射光线平行于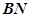 恰好在
恰好在 点发生全反射。已知
点发生全反射。已知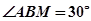 ,求
,求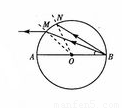
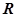 ,
,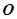 为球心,
为球心,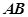 为直径。来自
为直径。来自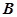 点的光线
点的光线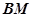 在
在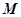 点射出。出射光线平行于
点射出。出射光线平行于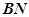 恰好在
恰好在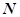 点发生全反射。已知
点发生全反射。已知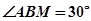 ,求
,求