题目内容
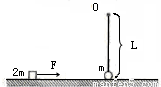
如图所示，长为L的不可伸长的绳子一端固定在O点，另一端系质量为m的小球，小球静止在光滑水平面上．现用大小为F水平恒力作用在另一质量为2m的物块上，使其从静止开始向右运动，一段时间后撤去该力，物块与小球发生正碰后速度变为原来的一半，小球恰好能在竖直平面内做圆周运动．已知重力加速度为g，小球和物体均可视为质点，试求：（1）小物块碰撞前速度V的大小；
（2）碰撞过程中系统损失的机械能；
（3）恒力F作用时间．
【答案】分析：（1）小球恰好通过最高点作圆周运动，根据牛顿第二定律求出临界速度，根据机械能守恒求出碰撞后速度．碰撞过程中，物块和小球系统动量守恒，求出小物块碰撞前速度V的大小．
（2）碰撞过程中系统损失的机械能就是系统动能的变化量．
（3）根据牛顿第二定律和运动学公式求出恒力F作用时间．
解答：解：（1）小球恰好通过最高点作圆周运动，此时重力刚好提供向心力，设速度为V，有
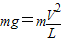
得V=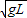
设小球碰撞后速度为V1，其后在摆至最高点过程中，机械能守恒：
mV12=
mV2+mg?2L
代入V值可得V1=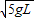
碰撞过程中，物块和小球系统动量守恒，有
2mV=mV1+2m?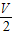
代入V1值可得V=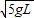
（2）碰撞过程中系统损失的机械能
△E=
?2m?V2-
?2m?
-
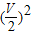mV12
代入所求出的速度值可得
△E=
mgL
（3）小球在水平面运动的加速度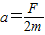
由速度公式V=at得力F作用时间
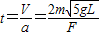
答：（1）小物块碰撞前速度V的大小是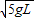
；
（2）碰撞过程中系统损失的机械能是
mgL；
（3）恒力F作用时间是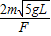
．
点评：本题关键明确各个运动过程，明确小球与小物块碰撞过程中系统动量守恒，要求同学们能正确进行受力，并能联想到已学的物理模型，根据相关公式解题．
（2）碰撞过程中系统损失的机械能就是系统动能的变化量．
（3）根据牛顿第二定律和运动学公式求出恒力F作用时间．
解答：解：（1）小球恰好通过最高点作圆周运动，此时重力刚好提供向心力，设速度为V，有
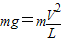
得V=
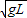
设小球碰撞后速度为V1，其后在摆至最高点过程中，机械能守恒：
mV12=mV2+mg?2L 代入V值可得V1=
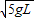
碰撞过程中，物块和小球系统动量守恒，有
2mV=mV1+2m?
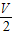
代入V1值可得V=
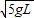
（2）碰撞过程中系统损失的机械能
△E=
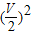?2m?V2-?2m?-mV12代入所求出的速度值可得
△E=
mgL （3）小球在水平面运动的加速度
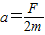
由速度公式V=at得力F作用时间
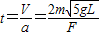
答：（1）小物块碰撞前速度V的大小是
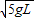；（2）碰撞过程中系统损失的机械能是
mgL；（3）恒力F作用时间是
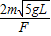．点评：本题关键明确各个运动过程，明确小球与小物块碰撞过程中系统动量守恒，要求同学们能正确进行受力，并能联想到已学的物理模型，根据相关公式解题．
练习册系列答案
名题金卷系列答案
相关题目
如图所示，长为L的轻杆一端固定一个质量为m的小球，另一端有光滑的固定轴O，现给球一初速度，使球和杆一起绕轴O在竖直平面内转动，不计空气阻力，则（ ）
（2005?潍坊模拟）如图所示，长为L的金属导线弯成一圆环，导线的两端接在电容为C的平行板电容器上，P、Q为电容器的两个极板，磁场垂直环面向里，磁感应强度以B=B0+Kt（K＞0）随时间变化t=0时，P、Q两板电势不相等．两板间的距离远小于环的半径，经时间t电容器P板（ ）
有一种叫“飞椅”的游乐项目，示意图如图所示，长为L的钢绳一端系着质量为m座椅，另一端固定在半径为r的水平转盘边缘，转盘可绕穿过其中心的竖直轴转动．当转盘以角速度ω匀速转动时，钢绳与转轴在同一竖直平面内，与竖直方向的夹角为θ，不计钢绳的重力，求：
如图所示，长为L的轻杆一端有一个小球，另一端有光滑的固定轴O．现在最低点给球一初速度2
如图所示，长为L的轻杆一端固定质量为m的小球，另一端有固定转轴O．现使小球在竖直平面内做圆周运动，P为圆周轨道的最高点，若小球通过圆周轨道最低点时的速度大小为