题目内容
3.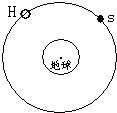 一组太空人乘坐太空穿梭机,去修理位于地球表面6.0×105m的圆形轨道上的哈勃太空望远镜H,机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜H在S前方数公里外,如图所示,设G为引力常量而M为地球质量,地球半径为R=6400Km,(9取9.8)回答下列问题:
一组太空人乘坐太空穿梭机,去修理位于地球表面6.0×105m的圆形轨道上的哈勃太空望远镜H,机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜H在S前方数公里外,如图所示,设G为引力常量而M为地球质量,地球半径为R=6400Km,(9取9.8)回答下列问题:(1)在穿梭机内,一质量为70㎏的太空人的视重是多少?
(2)计算轨道上的重力加速度及穿梭机在轨道上的速率和周期?(计算结果保留两位有效数字)
(3)穿梭机S能追上哈勃望远镜H吗?回答“能”还是“不能”,并说明道理.不能则提出解决方案.
分析 (1)穿梭机内的人处于完全失重状态,所以视重为零;
(2,3)根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、周期和向心力的表达式进行讨论即可.
解答 解:(1)穿梭机和里面的人受到的万有引力提供向心力,所以穿梭机内的人处于完全失重状态,所以视重为零.
(2)由mg=G$\frac{Mm}{r^2}$得:g′=$\frac{GM}{{{r^/}^2}}$;
所以:$\frac{g}{g^/}=\frac{r^2}{{{r^{/2}}}}=\frac{{{{({6.4×{{10}^6}})}^2}}}{{{{({6×{{10}^5}+6.4×{{10}^6}})}^2}}}$=0.84,
所以:g′=0.84g=0.84×9.8m/s2=8.2m/s2;
又由G$\frac{Mm}{r^2}$=m$\frac{v^2}{r}$得:v=$\sqrt{\frac{GM}{r}}$.
得:$\frac{v^/}{v}=\sqrt{\frac{r}{r^/}}=\sqrt{\frac{{6.4×{{10}^6}}}{{({6+64})×{{10}^5}}}}$=0.96m/s.
v′=0.96v=0.96×7.9km/s=7.6km/s.
由T=$\frac{{2π{r^/}}}{v^/}=\frac{{2×3.14×({6.4×{{10}^6}+6×{{10}^5}})}}{{7.6×{{10}^3}}}≈$5.8×103s.
(3)不能,结合(2)的计算可知,穿梭机和望远镜的速率一样.
答:(1)在穿梭机内,一质量为70㎏的太空人的视重是0;
(2)计算轨道上的重力加速度是8.2m/s2,穿梭机在轨道上的速率是7.6km/s,周期是5.8×103s;
(3)穿梭机不能追上哈勃望远镜,因为速率一样.
点评 本题关键抓住万有引力提供向心力,先列式求解出线速度、角速度、周期和加速度的表达式,再进行讨论

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案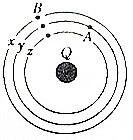 如图所示,Q为地球,A为空间运行的宇宙飞船,现有一对接舱B在A的后方加速追A,并与A实现对接,y轨道为A的运行轨道,x轨道和z轨道分别是比y轨道高一些和低一些的两个轨道,那么( )
如图所示,Q为地球,A为空间运行的宇宙飞船,现有一对接舱B在A的后方加速追A,并与A实现对接,y轨道为A的运行轨道,x轨道和z轨道分别是比y轨道高一些和低一些的两个轨道,那么( )| A. | B只有从x轨道开始加速,才有可能实现与A对接 | |
| B. | B只有从y轨道开始加速,才有可能实现与A对接 | |
| C. | B只有从z轨道开始加速,才有可能实现与A对接 | |
| D. | B从x、y轨道开始加速,都有可能实现与A对接,从z轨道开始加速,不能实现与A对接 |
 如图所示,两轮用皮带转动,皮带不打滑,图中有A、B、C三点,这三点所在处的半径rA>rB=rC,则以下有关各点线速度v、加速度ω的关系中正确的是( )
如图所示,两轮用皮带转动,皮带不打滑,图中有A、B、C三点,这三点所在处的半径rA>rB=rC,则以下有关各点线速度v、加速度ω的关系中正确的是( )| A. | vA=vB>vC | B. | vc>vA=vB | C. | ωc<ωA<ωB | D. | ωC=ωB>ωA |
| A. | 质点从 A 点到 B 点的平均速度为$\frac{{(v}_{A}{+v}_{B})}{2}$ | |
| B. | 质点从 A 点到 B 点的平均速度为$\frac{\sqrt{\frac{{{2a}_{1}a}_{2}L}{{(a}_{1}{+a}_{2})}}}{2}$ | |
| C. | 通过 C 点时的即时速度为$\sqrt{\frac{{{2a}_{1}a}_{2}L}{{(a}_{1}{+a}_{2})}}$ | |
| D. | AC:CB=a1:a2 |
| A. | 物体做简谐运动时,系统的机械能一定不守恒 | |
| B. | 简谐运动是非匀变速运动 | |
| C. | 物体做简谐运动的回复力一定是由合力提供的 | |
| D. | 秒摆的周期正好是1s |
| A. | 爱迪生 | B. | 普朗克 | C. | 牛顿 | D. | 伽利略 |
 某同学利用如图所示的装置探究功与速度变化的关系.
某同学利用如图所示的装置探究功与速度变化的关系.