题目内容
5. 竖直固定的轨道由半径为R的光滑$\frac{3}{4}$圆弧ABC和竖直粗糙杆CD构成,二者在C点相切,如图,一自然长度为$\sqrt{2}$R的轻质橡皮绳(其伸长时说的力学性质和理想弹簧相同)一端连接在A点,另一端于套在轨道上的质量为m的小圆环相连,今将圆环沿竖直轨道拉直E点,此时橡皮绳恰好处于自然长度,由此位置静止释放圆环,圆环沿轨道向下滑动,已知圆环在轨道CD上滑动时受到大小恒为f=$\frac{1}{2}$mg的摩擦力,当小环到达P点是速度最大,A,P连线与竖直直径AB夹角为θ=30°,小环滑动到最低点B时速度为v,求:
竖直固定的轨道由半径为R的光滑$\frac{3}{4}$圆弧ABC和竖直粗糙杆CD构成,二者在C点相切,如图,一自然长度为$\sqrt{2}$R的轻质橡皮绳(其伸长时说的力学性质和理想弹簧相同)一端连接在A点,另一端于套在轨道上的质量为m的小圆环相连,今将圆环沿竖直轨道拉直E点,此时橡皮绳恰好处于自然长度,由此位置静止释放圆环,圆环沿轨道向下滑动,已知圆环在轨道CD上滑动时受到大小恒为f=$\frac{1}{2}$mg的摩擦力,当小环到达P点是速度最大,A,P连线与竖直直径AB夹角为θ=30°,小环滑动到最低点B时速度为v,求:(1)小环从E点到C点的运动时间以及到达C点时的速度大小;
(2)运动中橡皮绳的最大弹性势能;
(3)小环到达B点时对轨道的压力大小(结果可用根式表示)
分析 (1)小环从E点到C点的过程,橡皮绳松驰,没有拉力.小环做匀加速运动.根据动能定理求出小球到达C点的速度,由位移等于平均速度乘以时间来求运动时间.
(2)小环运动到B点时橡皮绳的伸长量最大,弹性势能最大.由E到B过程,运用能量守恒定律求橡皮绳的最大弹性势能.
(3)小环到达P点是速度最大,其沿圆弧切线方向的合力为零,由此列式求出弹簧的劲度系数.在B点,由牛顿第二定律求出轨道对小环的支持力,再由牛顿第三定律得到小环对轨道的压力大小.
解答 解:(1)由E到C过程,橡皮绳松弛,有 h=2R
根据动能定理得
mgh-fh=$\frac{1}{2}m{v}_{0}^{2}$
解得,到达C点时的速度 v0=$\sqrt{2gR}$
由 2R=$\frac{{v}_{0}}{2}t$得
t=$\sqrt{\frac{8R}{g}}$
(2)B点时弹性势能最大,由E到B过程,由能量守恒定律得:
mg•3R-f•2R=$\frac{1}{2}m{v}^{2}$+Ep;
解得,橡皮绳的最大弹性势能 Ep=2mg-$\frac{1}{2}m{v}^{2}$;
(3)当小环到达P点是速度最大,在P点时,应有
mgsin60°=k(2Rcos30°-$\sqrt{2}$R)sin30°
得:k=$\frac{\sqrt{3}mg}{(\sqrt{3}-\sqrt{2})R}$
在B点,根据牛顿第二定律得:
k(2R-$\sqrt{2}$)R+N-mg=m$\frac{{v}^{2}}{R}$
得:N=mg+m$\frac{{v}^{2}}{R}$-$\frac{2\sqrt{3}-\sqrt{6}}{\sqrt{3}-\sqrt{2}}$mg
根据牛顿第三定律知,小环到达B点时对轨道的压力大小 N′=N=mg+m$\frac{{v}^{2}}{R}$-$\frac{2\sqrt{3}-\sqrt{6}}{\sqrt{3}-\sqrt{2}}$mg
答:
(1)小环从E点到C点的运动时间是$\sqrt{\frac{8R}{g}}$,到达C点时的速度大小是$\sqrt{2gR}$;
(2)运动中橡皮绳的最大弹性势能是2mg-$\frac{1}{2}m{v}^{2}$;
(3)小环到达B点时对轨道的压力大小是mg+m$\frac{{v}^{2}}{R}$-$\frac{2\sqrt{3}-\sqrt{6}}{\sqrt{3}-\sqrt{2}}$mg.
点评 本题关键是明确小环的受力情况、运动情况和能量转化情况,然后结合动能定理、功能关系、牛顿第二定律和向心力公式列式求解.

| A. | 原子核外轨道上的电子 | |
| B. | 原子核内所含的电子 | |
| C. | 原子核内中子变成质子时放出的电子 | |
| D. | 原子核内质子变成中子时放出的电子 |
| A. | 洛伦兹力的方向总是垂直于磁场的方向 | |
| B. | 洛伦兹力的方向可以不垂直于带电粒子的运动方向 | |
| C. | 洛伦兹力的大小与带电粒子的速度方向和磁场方向的夹角无关 | |
| D. | 仅将带电粒子的速度减半,洛伦兹力的大小变为原来的一半 |
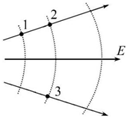
| A. | 同一电荷在1、2两点的所受电场力相同 | |
| B. | 同一电荷在2、3两点的所受电场力相同 | |
| C. | 负电荷从点1运动到点2,电场力做正功 | |
| D. | 负电荷从点1运动到点2和从点1运动到点3,增加的电势能相等 |
 如图所示,正方形单匝线框abcd的边长为L,每边电阻均为r,线框在磁感应强度为B的匀强磁场中以角速度ω绕cd轴从图示位置开始匀速转动,转轴与磁感线垂直.一理想电压表用电刷接在线框的c、d两点上,下列说法中不正确的是( )
如图所示,正方形单匝线框abcd的边长为L,每边电阻均为r,线框在磁感应强度为B的匀强磁场中以角速度ω绕cd轴从图示位置开始匀速转动,转轴与磁感线垂直.一理想电压表用电刷接在线框的c、d两点上,下列说法中不正确的是( )| A. | 电压表读数为$\frac{\sqrt{2}}{2}$BωL2 | |
| B. | 电压表读数为$\frac{\sqrt{2}}{8}$BωL2 | |
| C. | 从图示位置开始计时,流过线框电流的瞬时值表达式为i=$\frac{Bω{L}^{2}}{4r}$sinωt | |
| D. | 线框从图示位置转过$\frac{π}{2}$的过程中,流过cd边的电荷量为q=$\frac{B{L}^{2}}{r}$ |
| A. | 以小于第一宇宙速度的速度发射地球卫星也能发射成功 | |
| B. | 第一宇宙速度是物体在地面附近绕地球做匀速圆周运动的速度 | |
| C. | 第一宇宙速度是物体脱离地球引力的束缚,绕太阳运转的速度 | |
| D. | 第一宇宙速度是物体脱离太阳引力的束缚,飞到太阳系外的最小速度 |
| A. | 紫外线照射到金属锌板表面时能发生光电效应,则当增大紫外线的照射强度时,从锌板表面逸出的光电子的最大初动能也随之增大 | |
| B. | 波尔认为,原子中电子轨道是量子化的,能量也是量子化的 | |
| C. | .β射线是原子核外电子高速运动形成的 | |
| D. | 光子不仅具有能量,也具有动量 |
 如图所示,在光滑水平面上有一个质量为m的物体在恒定外力作用下做曲线运动,先后经过A、B、C三点,且A、B两点间距小于B、C两点间距,并且知道物体在B点速度最小,则( )
如图所示,在光滑水平面上有一个质量为m的物体在恒定外力作用下做曲线运动,先后经过A、B、C三点,且A、B两点间距小于B、C两点间距,并且知道物体在B点速度最小,则( )| A. | 物体经过A点速度大于经过C点速度 | |
| B. | 物体经过A点速度小于经过C点速度 | |
| C. | 物体经过A点速度可能等于经过C点速度 | |
| D. | 物体经过A点速度可能大于也可能小于经过C点速度 |
 在宇宙飞船上测物体的质量没有地球上那么容易.宇航员取来一个带孔的金属小球、一只弹簧测力计、一个带孔的内壁光滑的金属手柄、一段细尼龙线、一把刻度尺和一块秒表.他先将细尼龙线的一端打一个结,在线上标出一个位置并测出该标记点与结点间的距离L,然后将细尼龙线穿过金属小球(结点在球心处)和光滑金属手柄后连接到测力计上.现用手慢慢摇动手柄使金属球在如图(a)所示的平面内稳定转动时,细尼龙线的标记位置恰位于手柄上端口处,此时测力计的示数F如图(b)所示,同时另一宇航员用秒表记录了小球转动N圈所用的时间t,回答下列问题:
在宇宙飞船上测物体的质量没有地球上那么容易.宇航员取来一个带孔的金属小球、一只弹簧测力计、一个带孔的内壁光滑的金属手柄、一段细尼龙线、一把刻度尺和一块秒表.他先将细尼龙线的一端打一个结,在线上标出一个位置并测出该标记点与结点间的距离L,然后将细尼龙线穿过金属小球(结点在球心处)和光滑金属手柄后连接到测力计上.现用手慢慢摇动手柄使金属球在如图(a)所示的平面内稳定转动时,细尼龙线的标记位置恰位于手柄上端口处,此时测力计的示数F如图(b)所示,同时另一宇航员用秒表记录了小球转动N圈所用的时间t,回答下列问题: