题目内容
9．
如图所示，在第一象限内有垂直纸面向里的匀强磁场（磁场足够大），一对正、负电子分别以相同的速度沿与x轴成15°角的方向从原点垂直磁场射入，则负电子与正电子在磁场中运动的时间之比为（ ）| A． | 1：5 | B． | 5：2 | C． | 5：3 | D． | 3：2 |
分析 带电粒子以一定的速度垂直进入匀强磁场，在洛伦兹力的作用下做匀速圆周运动．粒子受到的洛伦兹力提供向心力；粒子在磁场中运动的周期仅与粒子的比荷及磁场有关，粒子速度的偏向角等于轨迹的圆心角θ，根据t=$\frac{θ}{2π}$T求运动时间．
解答 解：正电子进入磁场后，在洛伦兹力作用下向上偏转，而负电子在洛伦兹力作用下向下偏转．由T=$\frac{2πm}{qB}$，知两个电子的周期相等．
正电子从y轴上射出磁场时，根据几何知识得知，速度与y轴的夹角为75°，则正电子速度的偏向角为θ1=150°，其轨迹对应的圆心角也为150°，则正电子在磁场中运动时间为t1=$\frac{150°}{360°}$T，
同理，知负电子以15°入射，从x轴离开磁场时，速度方向与x轴的夹角为15°，则轨迹对应的圆心角为30°，负电子在磁场中运动时间为t2=$\frac{30°}{360°}$T．
所以负电子与正电子在磁场中运动时间之比为t1：t2=1：5．故A正确，BCD错误．
故选：A．
点评 带电粒子在磁场中运动的题目解题步骤为：定圆心、画轨迹、求半径．则可画出正、负离子运动轨迹，由几何关系可知答案．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
一圆环状玻璃砖截面如图所示，其内、外环半径分别为a、b且$\frac{a}{b}$=$\frac{\sqrt{3}}{3}$，一单色光以i=60°的入射角射入玻璃砖经一次反射后恰能沿原方向射出玻璃砖．
10．
如图所示，在“探究超重与失重的规律”实验中，某同学利用力传感器悬挂一个砝码在竖直方向运动时，拉力的大小随时间变化图象．0时刻，砝码处于静止状态，下列结论正确的是（ ）
如图所示，在“探究超重与失重的规律”实验中，某同学利用力传感器悬挂一个砝码在竖直方向运动时，拉力的大小随时间变化图象．0时刻，砝码处于静止状态，下列结论正确的是（ ）| A． | A时砝码处于超重，正向上加速运动 | |
| B． | B时砝码处于超重，正向下加速运动 | |
| C． | C时砝码处于失重，可能向下减速运动 | |
| D． | C时砝码处于超重，可能向下减速运动 |
17．
如图所示，光滑金属导轨ab和cd构成的平面与水平面成θ角，导轨间距Lac=2Lbd=2L，导轨电阻不计．两金属棒MN、PQ垂直导轨放置，与导轨接触良好．两棒质量mPQ=2mMN=2m，电阻RPQ=2RMN=2R，整个装置处在垂直导轨向上的磁感应强度为B的匀强磁场中，金属棒MN在平行于导轨向上的拉力，作用下沿导轨以速度v向上匀速运动，PQ棒恰好以速度v向下匀速运动．则（ ）
如图所示，光滑金属导轨ab和cd构成的平面与水平面成θ角，导轨间距Lac=2Lbd=2L，导轨电阻不计．两金属棒MN、PQ垂直导轨放置，与导轨接触良好．两棒质量mPQ=2mMN=2m，电阻RPQ=2RMN=2R，整个装置处在垂直导轨向上的磁感应强度为B的匀强磁场中，金属棒MN在平行于导轨向上的拉力，作用下沿导轨以速度v向上匀速运动，PQ棒恰好以速度v向下匀速运动．则（ ）| A． | MN中电流方向是由N到M | |
| B． | 匀速运动的速度v的大小是$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$ | |
| C． | 在MN、PQ都匀速运动的过程中，F=3mgsinθ | |
| D． | 在MN、PQ都匀速运动的过程中，F=2mgsinθ |
4．
如图所示，在纸面内半径为R的圆形区域中充满了垂直于纸面向里、磁感应强度为B的匀强磁场．一点电荷从图中A点以速度v0垂直磁场射入，速度方向与半径方向的夹角为30°．当该电荷离开磁场时，速度方向刚好改变了180°．不计电荷的重力，下列说法正确的是（ ）
如图所示，在纸面内半径为R的圆形区域中充满了垂直于纸面向里、磁感应强度为B的匀强磁场．一点电荷从图中A点以速度v0垂直磁场射入，速度方向与半径方向的夹角为30°．当该电荷离开磁场时，速度方向刚好改变了180°．不计电荷的重力，下列说法正确的是（ ）| A． | 该点电荷离开磁场时速度方向的反向延长线通过O点 | |
| B． | 该点电荷的比荷为$\frac{2{v}_{0}}{BR}$ | |
| C． | 该点电荷在磁场中的运动时间为$\frac{πR}{3{v}_{0}}$ | |
| D． | 该点电荷在磁场中的运动时间为$\frac{πR}{2{v}_{0}}$ |
14．
如图所示，直线ab是电场线中的一条电场线，从a点无初速度释放一电子，电子仅在电场力的作用下，沿直线从a点运动到b点，其电势能EP随位移x变化的规律如图乙所示．设a，b两点的电场强度大小分别为EA和EB，电势分别为φA和φB．则（ ）
如图所示，直线ab是电场线中的一条电场线，从a点无初速度释放一电子，电子仅在电场力的作用下，沿直线从a点运动到b点，其电势能EP随位移x变化的规律如图乙所示．设a，b两点的电场强度大小分别为EA和EB，电势分别为φA和φB．则（ ）| A． | EA=EB | B． | EA＜EB | C． | φA=φB | D． | φA＜φB |
1．
如图所示，光滑的绝缘圆轨道固定在光滑绝缘的水平桌面内，圆轨道所在空间存在水平方向的匀强电场，场强大小为E．一带电荷量为q的小球（可视为质点）沿轨道内侧做圆周运动．已知小球对轨道的压力的最大值为F1，对轨道的压力的最小值为F2，则F1-F2的值为（ ）
如图所示，光滑的绝缘圆轨道固定在光滑绝缘的水平桌面内，圆轨道所在空间存在水平方向的匀强电场，场强大小为E．一带电荷量为q的小球（可视为质点）沿轨道内侧做圆周运动．已知小球对轨道的压力的最大值为F1，对轨道的压力的最小值为F2，则F1-F2的值为（ ）| A． | 3qE | B． | 4qE | C． | 5qE | D． | 6qE |
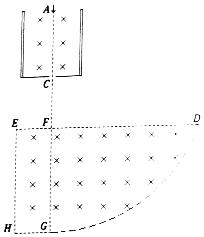如图所示，平行金属板竖直放置，底端封闭，中心线上开一小孔C，两板相距为d，电压为U．平行板间存在大小为B0的匀强磁场，方向垂直于纸面向里，AG是两板间的中心线．金属板下方存在有界匀强磁场区域EFDGH，EFGH为长方形，EF边长为$\frac{2a}{3}$；EH边长为2a，A、F、G三点共线，E、F、D三点共线，曲线GD是以3a为半径、以AG上某点（图中未标出）为圆心的一段圆弧，区域内磁场的磁感应强度大小为B，方向垂直于纸面向里．若大量带电粒子沿AG方向射入两金属板之间，有部分离子经F点进入下方磁场区域．不计重力，忽略离子间的相互作用．
19．
如图，在某电视台“水上闯关”节目中，一选手在平台上AB之间做初速度为零的匀加速直线运动，4s后平台边缘B点水平飞出，落在水中固定气垫上的C点，已知AB之间的距离为16m，平台与气垫上表面的竖直高度差H=1.8m，不计空气阻力，g=10m/s2，则对该选手下列说法正确的是（ ）
如图，在某电视台“水上闯关”节目中，一选手在平台上AB之间做初速度为零的匀加速直线运动，4s后平台边缘B点水平飞出，落在水中固定气垫上的C点，已知AB之间的距离为16m，平台与气垫上表面的竖直高度差H=1.8m，不计空气阻力，g=10m/s2，则对该选手下列说法正确的是（ ）| A． | 在AB阶段的加速度大小为1m/s2 | |
| B． | 在B点飞出时的速度大小为4m/s | |
| C． | 落在C点前一瞬间的速度大小为6m/s | |
| D． | 从B点到C点水平前进的距离为4.8m |