题目内容
11.甲、乙两车在同一直线轨道上同向行驶,甲车在前,速度为8m/s,乙车在后,速度为16m/s,当两车相距s=16m时,求:(1)甲车因故开始刹车,如果加速度大小为a=2m/s2,为避免两车相碰,乙车加速度至少为多大?
(2)甲车因故开始刹车,如果加速度大小为a=4m/s2,为避免两车相碰,乙车加速度至少为多大?
分析 (1)当乙车追上甲车速度恰好相等时,乙车刹车时加速度为最小值.再根据位移关系求解时间,根据速度相等条件求出加速度.
(2)当两车速度相等时,根据运动学公式求得时间,当甲、乙都已停止,则乙车以最小加速度行驶时刚好停止于甲车处,再根据位移关系求解.
解答 解:(1)设乙车的最小加速度为a',
当两车速度相等时,有:v甲+at=v乙+a't,
根据位移关系有:${v}_{甲}t+\frac{1}{2}a{t}^{2}+s={v}_{甲}t+\frac{1}{2}a'{t}^{2}$
联立两式,代入数据解得:a'=-4m/s2.
乙车加速度至少为4m/s2.
(2)设乙车的最小加速度为a″,
当两车速度相等时,有:v甲+at=v乙+a″t,
根据位移关系有:${v}_{甲}t+\frac{1}{2}a{t}^{2}+s={v}_{乙}t+\frac{1}{2}a''{t}^{2}$
联立两式,代入数据解得:t=4s,a″=-6m/s2.此时甲乙都已停止,则乙车以最小加速度行驶时刚好停止于甲车处.
则:$\frac{{v}_{乙}^{2}}{2a''}$=S+$\frac{{v}_{甲}^{2}}{2a}$
解得:a″=5.33 m/s2
故乙车加速度至少为5.33 m/s2.
答:(1)甲车因故开始刹车,如果加速度大小为a=2m/s2,为避免两车相碰,乙车加速度至少为4m/s2;
(2)甲车因故开始刹车,如果加速度大小为a=4m/s2,为避免两车相碰,乙车加速度至少为5.33 m/s2.
点评 本题是追及问题,关键是寻找相关条件.两个物体刚好不撞的条件:速度相等; 同时还要注意平均速度公式的应用,用平均速度求位移可以简化解题思路和过程.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
19. 如图,将一物块置于斜面上,并用一沿斜面方向的恒力F作用于物块上,斜面始终静止不动,则下列说法正确的有( )
如图,将一物块置于斜面上,并用一沿斜面方向的恒力F作用于物块上,斜面始终静止不动,则下列说法正确的有( )
 如图,将一物块置于斜面上,并用一沿斜面方向的恒力F作用于物块上,斜面始终静止不动,则下列说法正确的有( )
如图,将一物块置于斜面上,并用一沿斜面方向的恒力F作用于物块上,斜面始终静止不动,则下列说法正确的有( )| A. | 若物块静止不动,则物块受到斜面的摩擦力沿斜面向下 | |
| B. | 若物块静止不动,物块可能不受斜面的摩擦力 | |
| C. | 若物块沿斜面匀速上升,则斜面可能不受地面的摩擦力 | |
| D. | 若物块沿斜面匀速下滑,斜面受地面的摩擦力水平向左 |
6. 用阴极射线管可以观察电子在磁场中的运动径迹.图是阴极射线管的实物图,图中A、B两端的“+”“-”号表示阴极射线管工作时所接电源的极性,虚线表示电子的运动径迹,其中符合实际的是( )
用阴极射线管可以观察电子在磁场中的运动径迹.图是阴极射线管的实物图,图中A、B两端的“+”“-”号表示阴极射线管工作时所接电源的极性,虚线表示电子的运动径迹,其中符合实际的是( )
 用阴极射线管可以观察电子在磁场中的运动径迹.图是阴极射线管的实物图,图中A、B两端的“+”“-”号表示阴极射线管工作时所接电源的极性,虚线表示电子的运动径迹,其中符合实际的是( )
用阴极射线管可以观察电子在磁场中的运动径迹.图是阴极射线管的实物图,图中A、B两端的“+”“-”号表示阴极射线管工作时所接电源的极性,虚线表示电子的运动径迹,其中符合实际的是( )| A. |  | B. |  | C. |  | D. |  |
16.下列说法正确的是( )
| A. | 位移是描述物体位置变化大小的物理量 | |
| B. | 速度是物体运动的路程与所用时间的比值 | |
| C. | 在生活中能找到质点这样的物体 | |
| D. | 加速度是描述速度变化快慢及方向的物理量 |
20.一质点沿某一条直线运动时的速度-时间图象如图所示,则以下说法中正确的是( )


| A. | 第1s末质点的速度改变方向 | B. | 第2s末质点的速度改变方向 | ||
| C. | 第2s末质点的位移为0 | D. | 第3s末质点的位移为0 |
1.以下关于重力的说法正确的是( )
| A. | 重力的作用点叫重心,物体的重心都在物体上 | |
| B. | 重力的施力物体是地球 | |
| C. | 同一物体在某处向上抛出后所受的重力较小,向下抛出后所受的重力较大 | |
| D. | 重力的方向总是竖直向下,所以地球上任何地方重力方向相同 |
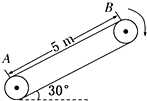 如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,现将一质量为m=5kg的小物体(可视为质点)轻放在传送带的A点,已知小物体与传送带之间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,在传送带将小物体从A点传送到B点的过程中,求:(g取10m/s2)
如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,现将一质量为m=5kg的小物体(可视为质点)轻放在传送带的A点,已知小物体与传送带之间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,在传送带将小物体从A点传送到B点的过程中,求:(g取10m/s2)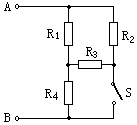 如图所示,R1=R2=R3=3Ω,R4=6Ω,UAB=12V,当S断开时,通过R1的电流为1A;当S闭合后,通过R1的电流为2.4A;R3消耗的功率为7.68W.
如图所示,R1=R2=R3=3Ω,R4=6Ω,UAB=12V,当S断开时,通过R1的电流为1A;当S闭合后,通过R1的电流为2.4A;R3消耗的功率为7.68W. 如图所示,一汽车停在小山坡底,突然司机发现在距坡底240m的山坡处泥石流以8m/s 的初速度、0.4m/s2的加速度匀加速倾泄而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动.已知司机发现泥石流的瞬间立即启动汽车,以0.5m/s2的加速度一直做匀加速直线运动.试分析汽车能否安全脱离?如能脱离危险,泥石流与汽车的最小距离为多少?
如图所示,一汽车停在小山坡底,突然司机发现在距坡底240m的山坡处泥石流以8m/s 的初速度、0.4m/s2的加速度匀加速倾泄而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动.已知司机发现泥石流的瞬间立即启动汽车,以0.5m/s2的加速度一直做匀加速直线运动.试分析汽车能否安全脱离?如能脱离危险,泥石流与汽车的最小距离为多少?