题目内容
14.某同学用探究动能定理的装置测滑块的质量M.如图甲所示,在水平气垫导轨上靠近定滑轮处固定一个光电门.让一带有遮光片的滑块自某一位置由静止释放,计时器可以显示出遮光片通过光电门的时间t(t非常小),同时用米尺测出释放点到光电门的距离s.
(1)该同学用螺旋测微器测出遮光片的宽度d如图乙所示,则d=1.880mm.
(2)实验中多次改变释放点,测出多组数据,描点连线,做出的图象为一条倾斜直线,如图丙所示.图象的纵坐标s表示释放点到光电门的距离,则横坐标表示的是D.
A.t B.t2 C.$\frac{1}{t}$ D.$\frac{1}{{t}^{2}}$
(3)已知钩码的质量为m,图丙中图线的斜率为k,重力加速度为g.根据实验测得的数据,写出滑块质量的表达式M=$\frac{2kmg}{{d}^{2}}-m$.(用字母表示)
分析 (1)螺旋测微器的读数等于固定刻度读数加上可动刻度读数,需估读.
(2)根据极短时间内的平均速度等于瞬时速度得出滑块通过光电门的瞬时速度,根据动能定理抓住钩码重力做功等于系统动能的增加量列出表达式,从而确定横坐标表示的物理量.
(3)结合表达式得出图线斜率k的含义,从而求出滑块质量M的表达式.
解答 解:(1)螺旋测微器的固定刻度读数为1.5mm,可动刻度读数为0.01×38.0mm=0.380mm,则最终读数为1.880mm.
(2)滑块通过光电门的瞬时速度v=$\frac{d}{t}$,根据动能定理得,mgs=$\frac{1}{2}(M+m){v}^{2}=\frac{1}{2}(M+m)\frac{{d}^{2}}{{t}^{2}}$,则$s=\frac{(M+m){d}^{2}}{2mg}•\frac{1}{{t}^{2}}$,因为图线为线性关系图线,可知横坐标表示$\frac{1}{{t}^{2}}$.故选:D.
(3)由$s=\frac{(M+m){d}^{2}}{2mg}•\frac{1}{{t}^{2}}$知,图线的斜率k=$\frac{(M+m){d}^{2}}{2mg}$,解得滑块质量M=$\frac{2kmg}{{d}^{2}}-m$.
故答案为:(1)1.880,(2)D,(3)$\frac{2kmg}{{d}^{2}}-m$.
点评 解决本题的关键掌握螺旋测微器的读数方法,对于图线问题,一般的解题思路是通过物理规律得出两个物理量的关系式,结合图线的斜率或截距进行求解.

练习册系列答案
相关题目
4.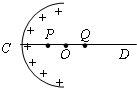 已知均为带电球壳内部的电场强度处处为零.将球壳一分为二,取其一半如图所示,所带电荷仍均匀分布在半球面上.CD为通过半球顶点C与球心O的直线,半球壳关于CD对称.P、Q为CD上在O点两侧与O点距离相等的两点.则下列判断正确的是( )
已知均为带电球壳内部的电场强度处处为零.将球壳一分为二,取其一半如图所示,所带电荷仍均匀分布在半球面上.CD为通过半球顶点C与球心O的直线,半球壳关于CD对称.P、Q为CD上在O点两侧与O点距离相等的两点.则下列判断正确的是( )
 已知均为带电球壳内部的电场强度处处为零.将球壳一分为二,取其一半如图所示,所带电荷仍均匀分布在半球面上.CD为通过半球顶点C与球心O的直线,半球壳关于CD对称.P、Q为CD上在O点两侧与O点距离相等的两点.则下列判断正确的是( )
已知均为带电球壳内部的电场强度处处为零.将球壳一分为二,取其一半如图所示,所带电荷仍均匀分布在半球面上.CD为通过半球顶点C与球心O的直线,半球壳关于CD对称.P、Q为CD上在O点两侧与O点距离相等的两点.则下列判断正确的是( )| A. | P点电场强度大于Q点电场强度 | |
| B. | P点电势高于Q点电势 | |
| C. | 将与带正电微粒沿直线从P点移到到Q点,电场力先做正功后做负功 | |
| D. | 将与带负电微粒从Q点由静止释放,仅在电场力作用下,微粒向P做匀加速运动 |
5.有A、B两个弹簧振子,A的固有频率为f,B的固有频率为4f,如果它们都在频率为2f的驱动力作用下做受迫振动,那么下列结论中正确的是( )
| A. | 振子A的振幅较大,振动频率为f | B. | 振子B的振幅较大,振动频率为2f | ||
| C. | 振子A的振幅较大,振动频率为2f | D. | 振子B的振幅较大,振动频率为4f |
2.某同学在做“探究弹簧的弹力与伸长的关系”实验中,利用了如图甲所示的实验装置.通过在悬挂的弹簧下面加挂钩码,逐渐使弹簧伸长,得到的数搌记录在以下的表格中.
A.请你根据数据在图乙的坐标中画出F-x图线;
B.由图线得到结论:弹簧的弹力与伸长量成正比
C.由图线得出弹簧的劲度系数k=43 N/m.(取两位有效数字)

| 钩码个数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 弹簧弹力F(N) | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 |
| 弹簧伸长x(cm) | 1.20 | 2.40 | 3.60 | 4.76 | 6.10 | 7.10 |
B.由图线得到结论:弹簧的弹力与伸长量成正比
C.由图线得出弹簧的劲度系数k=43 N/m.(取两位有效数字)

9.下列说法正确的是( )
| A. | 对于一定质量的理想气体,若气体的压强和体积都发生变化,其内能可能不变 | |
| B. | 对于密封在容积不变的容器内的理想气体,若气体温度升高,则气体一定从外界吸热 | |
| C. | 脱脂棉脱脂的目的,在于使它从不能被水浸润变为可以被水浸润,以便吸取药液 | |
| D. | 悬浮在液体中的微粒越大,在某一瞬间跟它相撞的液体分子数越多,撞击作用的不平衡性就表现得越明显 | |
| E. | 液体表面存在着张力是因为液体内部分子间的距离大于液体表面层分子间的距离 |
19.“嫦娥三号”在月球表面释放出“玉兔”号月球车开展探测工作,若该月球车质量为m,已知地球半径为R1,月球半径为R2,地球和月球表面处的重力加速度分别为g和g月,下列说法正确是( )
| A. | 若在月球表面用弹簧秤称该月球车,示数为零 | |
| B. | 若在月球表面用弹簧秤称该月球车,示数为mg月 | |
| C. | 地球与月球的质量之比为$\frac{g{{R}_{1}}^{2}}{{g}_{月}{{R}_{2}}^{2}}$ | |
| D. | 卫星在很靠近地球和月球表面的轨道上做匀速圆周运动的周期之比为$\sqrt{\frac{g{{R}_{1}}^{3}}{{g}_{月}{{R}_{2}}^{3}}}$ |
6.利用重物下落验证机械能守恒定律的实验中,下面叙述正确的是( )
| A. | 应该用天平称出重物的质量 | |
| B. | 必须选用点迹清晰,特别是第一点没有拉成长条的纸带 | |
| C. | 操作时应在接通电源的同时放开纸带 | |
| D. | 电磁打点计时器应接在电压为4~6V的交流电源上 |
9.质量为w的物体由静止开始自由下落,由于空气阻力作用,下落的加速度为0.8g,在物体下落A的过程中,下列说法中正确的是( )
| A. | 重力对物体做功0.8mgh | B. | 物体的重力势能减少了0.8mgh | ||
| C. | 物体下落前的重力势能是0.8mgh | D. | 物体的动能增加了0.8mgh |
 如图所示,光滑水平面上的同一直线上放着处于静止状态的光滑曲面体B和滑块C,B的质量为3m,C的质量为2m,B开始处于锁定状态,一质量为m的小球A从曲面上离地面高h处由静止释放,沿曲面滚到水平面上再与滑块发生弹性碰撞,小球滚离曲面体后,立即让曲面体解除锁定,小球被滑块反弹后再滑上曲面体,重力加速度为g,求:
如图所示,光滑水平面上的同一直线上放着处于静止状态的光滑曲面体B和滑块C,B的质量为3m,C的质量为2m,B开始处于锁定状态,一质量为m的小球A从曲面上离地面高h处由静止释放,沿曲面滚到水平面上再与滑块发生弹性碰撞,小球滚离曲面体后,立即让曲面体解除锁定,小球被滑块反弹后再滑上曲面体,重力加速度为g,求: