题目内容
如图所示，MN和PQ为竖直方向两平行长直金属导轨，间距L为0.40m，电阻不计，导轨所在平面与磁感应强度B为0.50T的匀强磁场垂直，质量m为6.0×10-3kg、电阻为1.0Ω的金属杆ab始终垂直于导轨，并与其保持光滑接触。导轨两端分别接有滑动变阻器和阻值为3.0Ω的电阻R1。当杆ab达到稳定状态时以速度V匀速下滑，整个电路消耗的电功率P为0.27W，重力加速度取10 m/s2，试求速率V和滑动变阻器接入电路部分的阻值R2
R2为6Ω
解析试题分析：下滑过程中ab棒产生的感应电动势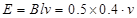
，
由于金属棒匀速下滑，根据右手定则知ab的感应电流从a到b，根据左手定则ab受到竖直向上安培力：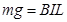
，
则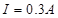
整个电路消耗功率P=0.27W，
所以金属棒切割磁感线产生共功率为P=IE=0.27W，
联立则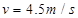
则电动势E=BLV=0.9V，
电流，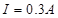
所以总电阻为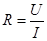
，
且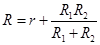
，
则连入电路部分的电阻为R2=6Ω
考点：电磁感应定律、闭合电路欧姆定律
点评：本题通过电磁感应定律求出感应电动势，从而利用闭合电路欧姆定律求出并联电阻。
练习册系列答案
相关题目
（2013?天津模拟）如图所示，MN和PQ为固定在绝缘水平面上两平行光滑金属导轨，导轨左端MP间接有阻值为R1=2Ω导线；导轨右端接有与水平轨道相切、半径r=0.5m内壁光滑的半圆金属轨道．导轨间距L=0.4m，电阻不计．导轨所在平面abcd区域内有竖直向上B=0.5T的匀强磁场．导轨上长度也为0.4m、质量m=0.6kg、电阻R2=1Ω的金属棒AB以v0=6m/s速度进入磁场区域，离开磁场区域后恰好能到达半圆轨道的最高点，运动中金属棒始终与导轨保持良好接触．已知重力加速度g=10m/s2．求：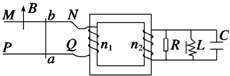
如图所示，MN和PQ为两个光滑的电阻不计的水平金属导轨，变压器为理想变压器，今在水平导轨部分加一竖直向上的匀强磁场，则以下说法正确的是（ ）
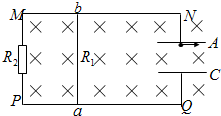如图所示，MN和PQ是相距40cm的平行金属导轨，一根电阻R1=3Ω的金属棒ab可紧贴平行导轨运动，两块相互平行，相距20cm且水平放置的金属板A和C分别与两平行导轨相连接，图中跨接在ab间的电阻R2=1Ω，导轨和连接导线的电阻可忽略不计，先将整个装置放在图示的匀强磁场中，当导体棒ab以速率v匀速沿导轨运动时，能使一个质量为m、带电量为q的负电微粒也以速率v在两金属板空间做匀速圆周运动而不触及两板．求：
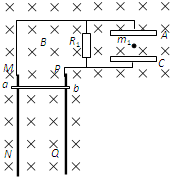（2006?河东区二模）如图所示，MN和PQ是竖直放置相距1m的光滑平行金属导轨，（导轨足够长，电阻不计），其上方连有R1=9Ω的电阻和两块水平放置相距d=20cm的平行金属板，A、C，金属板长L=1m，将整个装置放置在如图所示的方向垂直纸面向里的匀强磁场中，磁感应强度B=1T，现使电阻R2=1Ω的金属棒ab与导轨MN、PQ接触，并由静止释放，当其下落h=10m时恰能匀速运动（运动中ab棒始终保持水平状态，且与导轨接触良好），此时将一质量m1=0.45g，带电荷量q=1.0×10-4C的微粒放置在A、C金属板的正中央，微粒恰好静止，（g=10m/s2，设两板间的电场为匀强电场），求：
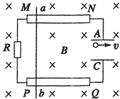如图所示，MN和PQ是相距l=40cm的平行金属导轨，一根电阻r=0.3Ω的金属棒ab可紧贴平行导轨运动．两块相互平行，相距d=20cm，且水平放置的金属板A和C分别与两金属导轨相连接，图中跨接在两导轨间的电阻R=0.1Ω，导轨和连接导线的电阻均可忽略不计．现将整个装置放置在图示的匀强磁场中，当导体棒ab以速率v匀速沿导轨运动时，恰能使一个带负电的微粒也以速率v在两金属板间做匀速圆周运动．重力加速度g取10m/s2，求：