题目内容
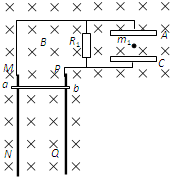 (2006?河东区二模)如图所示,MN和PQ是竖直放置相距1m的光滑平行金属导轨,(导轨足够长,电阻不计),其上方连有R1=9Ω的电阻和两块水平放置相距d=20cm的平行金属板,A、C,金属板长L=1m,将整个装置放置在如图所示的方向垂直纸面向里的匀强磁场中,磁感应强度B=1T,现使电阻R2=1Ω的金属棒ab与导轨MN、PQ接触,并由静止释放,当其下落h=10m时恰能匀速运动(运动中ab棒始终保持水平状态,且与导轨接触良好),此时将一质量m1=0.45g,带电荷量q=1.0×10-4C的微粒放置在A、C金属板的正中央,微粒恰好静止,(g=10m/s2,设两板间的电场为匀强电场),求:
(2006?河东区二模)如图所示,MN和PQ是竖直放置相距1m的光滑平行金属导轨,(导轨足够长,电阻不计),其上方连有R1=9Ω的电阻和两块水平放置相距d=20cm的平行金属板,A、C,金属板长L=1m,将整个装置放置在如图所示的方向垂直纸面向里的匀强磁场中,磁感应强度B=1T,现使电阻R2=1Ω的金属棒ab与导轨MN、PQ接触,并由静止释放,当其下落h=10m时恰能匀速运动(运动中ab棒始终保持水平状态,且与导轨接触良好),此时将一质量m1=0.45g,带电荷量q=1.0×10-4C的微粒放置在A、C金属板的正中央,微粒恰好静止,(g=10m/s2,设两板间的电场为匀强电场),求:(1)微粒带何种电荷?ab棒的质量m2为多少?
(2)金属棒自静止释放到刚好匀速运动的过程中,损失的机械能为多少?
(3)若使微粒突然获得竖直向下的初速度v0,但运动过程中不能碰到金属板,对初速度v0有何要求?该微粒第一次发生大小为
| ||
| Bq |
分析:(1)微粒恰好静止在金属板间,电场力与重力平衡,由平衡条件列式求出AC板间电压.ab棒向下匀速运动时,切割产生感应电动势,相当于电源,金属板间的电压等于电阻R1两端的电压,由欧姆定律可求出电路中的感应电流.根据棒ab匀速运动,由安培力与重力平衡列式,即可求得ab棒的质量m2.
(2)金属棒自静止释放到刚好匀速运动的过程中,损失的机械能转化为电路中的电能,根据能量守恒求解.
(2)使微粒突然获得竖直向下的初速度v0,带电微粒将在正交的电磁场中做匀速圆周运动,运动半径不大于
,就碰不到金属板,由半径公式求初速度.根据位移,分析时间与周期的关系,求时间.
(2)金属棒自静止释放到刚好匀速运动的过程中,损失的机械能转化为电路中的电能,根据能量守恒求解.
(2)使微粒突然获得竖直向下的初速度v0,带电微粒将在正交的电磁场中做匀速圆周运动,运动半径不大于
| d |
| 2 |
解答:解:(1)微粒带正电;因微粒静止,Eq=m1g
又E=
得
q=m1g,解得U=9V
根据欧姆定律得:U=IR1
解得I=1A
因棒能匀速运动,有:BIL1=m2g
把数据带入上各式得 m2=0.1kg
(2)损失的机械能为:△E=mgh-
mv2
v=
代入数据解得△E=5J
(3)带电微粒在正交的电磁场中做匀速圆周运动,运动半径不大于
,有:
≤
解得 v0≤
m/s
发生该位移的时间为 t=
微粒圆周运动的周期 T=
解得 t=
s
答:
(1)微粒带正电,ab棒的质量m2为0.1kg.
(2)金属棒自静止释放到刚好匀速运动的过程中,损失的机械能为5J.
(3)微粒第一次发生大小为
的位移,需要的时间是
s.
又E=
| U |
| d |
得
| U |
| d |
根据欧姆定律得:U=IR1
解得I=1A
因棒能匀速运动,有:BIL1=m2g
把数据带入上各式得 m2=0.1kg
(2)损失的机械能为:△E=mgh-
| 1 |
| 2 |
v=
| I(R1+R2) |
| BL1 |
代入数据解得△E=5J
(3)带电微粒在正交的电磁场中做匀速圆周运动,运动半径不大于
| d |
| 2 |
| m1v0 |
| qB |
| d |
| 2 |
解得 v0≤
| 1 |
| 45 |
发生该位移的时间为 t=
| T |
| 4 |
微粒圆周运动的周期 T=
| 2πm1 |
| qB |
解得 t=
| 9π |
| 4 |
答:
(1)微粒带正电,ab棒的质量m2为0.1kg.
(2)金属棒自静止释放到刚好匀速运动的过程中,损失的机械能为5J.
(3)微粒第一次发生大小为
| 2 |
| m1v0 |
| qB |
| 9π |
| 4 |
点评:本题是电磁感应与带电粒子在复合场中平衡和圆周运动的综合,关键要抓住它们之间的联系,并掌握电磁学的基本规律求解.

练习册系列答案
相关题目
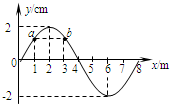 (2006?河东区二模)如图所示,一列简谐波以8.0m/s的速度传播,某一时刻波上有ab两质点,位移大小相等,方向相同,以下说法正确的是( )
(2006?河东区二模)如图所示,一列简谐波以8.0m/s的速度传播,某一时刻波上有ab两质点,位移大小相等,方向相同,以下说法正确的是( )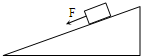 (2006?河东区二模)物体恰能在一个斜面上沿斜面匀速下滑,可以证明出此时斜面不受地面的摩擦力作用,若沿斜面方向用力向下推此物体,使物体加速下滑,则斜面受地面的摩擦力和地面的支持力,下列说法正确的是( )
(2006?河东区二模)物体恰能在一个斜面上沿斜面匀速下滑,可以证明出此时斜面不受地面的摩擦力作用,若沿斜面方向用力向下推此物体,使物体加速下滑,则斜面受地面的摩擦力和地面的支持力,下列说法正确的是( ) (2006?河东区二模)如图所示的一个匝数为10匝的矩形线圈在匀强磁场中绕垂直于磁场的轴匀速转动,周期为T,若用交流电压表测得a、b两点间的电压为20.0V,则可知:若从中性面开始计时,当t=
(2006?河东区二模)如图所示的一个匝数为10匝的矩形线圈在匀强磁场中绕垂直于磁场的轴匀速转动,周期为T,若用交流电压表测得a、b两点间的电压为20.0V,则可知:若从中性面开始计时,当t=