题目内容
20. 如图所示,一质量m=2kg的物体从离地面高h=0.8m处水平抛出,恰能无碰撞第沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑.圆弧AB和四分之一圆弧CD与水平固定BC相切,已知θ=53°,圆弧AB半径为R=1.0m,BC部分与物体的摩擦因素μ=0.4,BC段长度为3m,其余部分均为光滑面(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6).求:
如图所示,一质量m=2kg的物体从离地面高h=0.8m处水平抛出,恰能无碰撞第沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑.圆弧AB和四分之一圆弧CD与水平固定BC相切,已知θ=53°,圆弧AB半径为R=1.0m,BC部分与物体的摩擦因素μ=0.4,BC段长度为3m,其余部分均为光滑面(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6).求:(1)物体水平抛出的速度v?
(2)物体运动到圆弧轨道最低点B时对轨道的压力?
(3)物块最终静止在哪个位置?
分析 (1)物体从平台飞出后做的是平抛运动,根据平抛运动在竖直方向上是自由落体运动,可以求得运动的时间,得到物体通过A点的竖直分速度,再根据速度的分解求解
初速度v.
(2)从A点开始物体做的是圆周运动,由机械能守恒求出物体经过B点的速度,根据向心力的公式可以求得在B点时受到的支持力的大小,再由牛顿第三定律得到压力.
(3)由于物体克服摩擦力做功,机械能不断减小,最终停在BC上,设在BC上运动的总路程是S,对全程运用动能定理求出S,即可确定位置.
解答 解:(1)物体做平抛运动的过程,据平抛运动的规律可得
通过A点时的竖直分速度 vy=$\sqrt{2gh}$=$\sqrt{2×10×0.8}$=4m/s
据题知物体通过A点时速度沿A点的切线方向,与水平方向的夹角为53°
则根据速度的分解可知:v=vycot53°=4×$\frac{3}{4}$m/s=3m/s
(2)物体从抛出到B的过程,由机械能守恒得
mgh+mgR(1-cos53°)=$\frac{1}{2}m{v}_{B}^{2}$-$\frac{1}{2}m{v}^{2}$
在B点,有 N-mg=m$\frac{{v}_{B}^{2}}{R}$
联立解得${v}_{B}^{\;}$=2$\sqrt{10}$m/s,N=100N
根据牛顿第三定律知,物体运动到圆弧轨道最低点B时对轨道的压力为100N.
(3)设在BC上运动的总路程是S,对全程运用动能定理得:
-μmgS=0-$\frac{1}{2}m{v}_{B}^{2}$
解得 S=5m
因为BC段长度为3m,所以物体最终停在BC上离B点3m处.
答:
(1)物体水平抛出的速度v是4m/s.
(2)物体运动到圆弧轨道最低点B时对轨道的压力是100N.
(3)物块最终静止在BC上离B点3m处.
点评 解决本题的关键要把握每个过程的规律,特别是要明确摩擦力作功与总路程有关,运用动能定理对整个过程列式,可求出总路程.

 名题金卷系列答案
名题金卷系列答案| A. | 12N,15N,18N | B. | 20N,40N,65N | C. | 3N,6N,8N | D. | 3N,10N,15N |
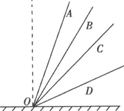 如图所示,有一系列斜面处在同一竖直面上,都位于竖直线OO′的右侧,倾角不同,它们的底端都是O点,有一些完全相同的滑块(可视为质点)从这些斜面上的A、B、C、D…各点同时由静止释放,下列判断正确的是( )
如图所示,有一系列斜面处在同一竖直面上,都位于竖直线OO′的右侧,倾角不同,它们的底端都是O点,有一些完全相同的滑块(可视为质点)从这些斜面上的A、B、C、D…各点同时由静止释放,下列判断正确的是( )| A. | 若各斜面均光滑,且这些滑块到达0点的速率相同,则A、B、C、D…各点处在同一竖直线上 | |
| B. | 若各斜面均光滑,且这些滑块到达0点所用时间相等,则A、B、C、D…各点处在同一圆周上 | |
| C. | 若各斜面与这些滑块之间的动摩擦因数相同,滑到O点的过程中,各滑块损失的机械能相同,则A、B、C、D…各点处在同一竖直线上 | |
| D. | 若各斜面与这些滑块之间的动摩擦因数相同,滑到O点的过程中,各滑块损失的机械能相同,则A、B、C、D…各点处在同一圆周上 |
 一小球在外力F的作用下由A运动到B,外力F对小球做功20J,小球克服重力做功10J,克服弹力做功5J,则( )
一小球在外力F的作用下由A运动到B,外力F对小球做功20J,小球克服重力做功10J,克服弹力做功5J,则( )| A. | 小球在A点的重力势能比B点大10J | |
| B. | 小球在A点的动能比B点小5J | |
| C. | 从A点到B点过程中,小球机械能增加15J | |
| D. | 小球和弹簧组成的系统机械能守恒 |
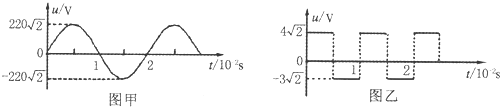
| A. | 图甲表示交流电,图乙表示直流电 | |
| B. | 图乙所示电压的有效值为5V | |
| C. | 将图甲电压通过一个理想二极管给电阻供电,电压的有效值变为110V | |
| D. | 图甲所示电压经匝数比为10:1的变压器变压后,频率变为原来的$\frac{1}{10}$ |
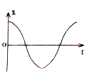
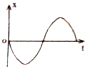
 一个弹簧振子在A、B间作简谐运动,O为平衡位置,如图甲所示,假设向右为正方向,当振子向左运动经过O点时开始计时,则图乙中画出的振动图象正确的是( )
一个弹簧振子在A、B间作简谐运动,O为平衡位置,如图甲所示,假设向右为正方向,当振子向左运动经过O点时开始计时,则图乙中画出的振动图象正确的是( )

 某电视台“快乐向前冲”节目中的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,加速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器,可以在电动机带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置放手,才能顺利落在转盘上.设人的质量为m(不计身高大小),人与转盘间的最大静摩擦力为μmg,重力加速度为g.
某电视台“快乐向前冲”节目中的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,加速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器,可以在电动机带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置放手,才能顺利落在转盘上.设人的质量为m(不计身高大小),人与转盘间的最大静摩擦力为μmg,重力加速度为g. 如图所示,质量为M、倾角为α的斜劈静止在水平地面上,在斜劈的粗糙斜面上,有质量分别为m、2m的A、B两个物体,中间用轻杆相连,它们以某一初速沿斜面向上运动,斜劈始终保持静止,斜面和物体间动摩擦因数均为μ,重力加速度大小为g,则在它们向上运动过程,杆中的张力大小为0,水平地面对斜劈底部的支持力大小为Mg+3mgcos2α-3μmgsinαcosα.
如图所示,质量为M、倾角为α的斜劈静止在水平地面上,在斜劈的粗糙斜面上,有质量分别为m、2m的A、B两个物体,中间用轻杆相连,它们以某一初速沿斜面向上运动,斜劈始终保持静止,斜面和物体间动摩擦因数均为μ,重力加速度大小为g,则在它们向上运动过程,杆中的张力大小为0,水平地面对斜劈底部的支持力大小为Mg+3mgcos2α-3μmgsinαcosα.