题目内容
19. 如图所示,一根张紧的水平弹性长绳上的a、b两点,相距14.0m,b点在a点的右方.当一列简谐横波沿此绳向右传播时,若a点的位移达到正向最大时,b点的位移恰为零,且向下运动.经过1.00s后,a点的位移为零,且向下运动,而b点的位移恰达到负极大(T>1.00s).则这简谐横波的波速可能等于( )
如图所示,一根张紧的水平弹性长绳上的a、b两点,相距14.0m,b点在a点的右方.当一列简谐横波沿此绳向右传播时,若a点的位移达到正向最大时,b点的位移恰为零,且向下运动.经过1.00s后,a点的位移为零,且向下运动,而b点的位移恰达到负极大(T>1.00s).则这简谐横波的波速可能等于( )| A. | 14m/s | B. | 3.5m/s | C. | 2m/s | D. | 1m/s |
分析 根据a、b两点的状态,分析它们平衡位置之间的距离与波长的关系.当a点的位移达到正极大值时,b点的位移恰为0,且向下运动,a、b平衡位置间距离至少等于$\frac{3}{4}$波长,根据波的周期性,得出波长的通项.根据经过1s后,a点的位移为0,且向下运动,而b点的位移恰达到负极大值,得出时间与周期的关系式,得到周期的通项,求出波速的通项,再求解波速的特殊值.
解答 解:由题,当a点的位移达到正极大值时,b点的位移恰为0,且向下运动,得到xab=(n+$\frac{3}{4}$)λ,n=0,1,2,…
根据题意,经过1s后,a点的位移为0,且向下运动,而b点的位移恰达到负极大值,则有t=(k+$\frac{1}{4}$)T,由于T>1.00s,k只能取0.
则得到波长λ=$\frac{4{x}_{ab}}{4n+3}$,T=4t,波速v=$\frac{λ}{T}$=$\frac{14}{4n+3}$m/s
当n=0时,v=$\frac{14}{3}$m/s=4.67m/s;
当n=1时,v=2m/s;
当n=2时,v=$\frac{14}{11}$m/s
当n=3时,v=$\frac{14}{15}$m/s
故C正确;ABD错误.
故选:C
点评 本题要考虑空间的周期性和时间的周期性,列出两个波长和周期的通项,再求解特殊值.中等难度.

练习册系列答案
相关题目
4. 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )| A. | 机械能均逐渐减小 | B. | 经最低点时动能相等 | ||
| C. | 均能到达半圆形槽右边缘最高点 | D. | 机械能总是相等的 |
11.理发用的电吹风机中有电动机和电热丝,电动机带动风叶转动,电热丝给空气加热,得到热风将头发吹干.设电动机线圈的电阻为R1,它与电热丝的电阻R2相串联,接到电源上时,电吹风机两端电压为U,电流为I,消耗的电功率为P,则有( )
| A. | P=I2(R1+R2) | B. | P=IU | C. | P=$\frac{{U}^{2}}{({R}_{1}+{R}_{2})}$ | D. | P>I2(Rl+R2) |
9.如图所示的链球、铅球、铁饼和标枪都是奥运会田径项目,当把这些物体斜向上抛出后,不计空气阻力,则这些物体从被抛出到落地的过程中( )


| A. | 物体的动能一定增大,重力势能一定减小 | |
| B. | 物体的动能一直减小,重力势能一直增大 | |
| C. | 物体的动能先减小后增大,重力势能先增大后减小 | |
| D. | 物体的动能先增大后减小,重力势能先减小后增大 |
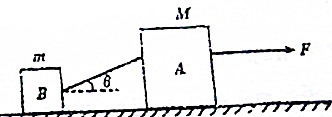 如图所示,在水平上放A、B两物体,质量分别为M和m,且M>m,它们与地面的动摩擦因数为μA、μB,且μA>μB,用一细绳连接,绳与水平方向成θ角,在A物体上加一水平拉力,使它们做匀速直线运动,细绳在物体A上的连接点可以上下移动调节,使得θ的大小可以在0°≤θ<90°的范围内变化,重力加速度为g,求:
如图所示,在水平上放A、B两物体,质量分别为M和m,且M>m,它们与地面的动摩擦因数为μA、μB,且μA>μB,用一细绳连接,绳与水平方向成θ角,在A物体上加一水平拉力,使它们做匀速直线运动,细绳在物体A上的连接点可以上下移动调节,使得θ的大小可以在0°≤θ<90°的范围内变化,重力加速度为g,求:
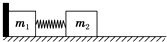 如图所示,两个木块的质量分别为m1=0.2kg、m2=0.6kg,中间用轻弹簧相连接放在光滑的水平面上,且m1左侧靠一固定竖直挡板.某一瞬间敲击木块m2使其获得2m/s水平向左的速度,木块m2向左压缩弹簧然后被弹簧弹回,弹回时带动木块m1运动.求:
如图所示,两个木块的质量分别为m1=0.2kg、m2=0.6kg,中间用轻弹簧相连接放在光滑的水平面上,且m1左侧靠一固定竖直挡板.某一瞬间敲击木块m2使其获得2m/s水平向左的速度,木块m2向左压缩弹簧然后被弹簧弹回,弹回时带动木块m1运动.求: