题目内容
3.小球从空中以某一初速度水平抛出,落地前1s时刻,速度方向与水平方向夹30°角,落地时速度方向与水平方向夹60°角,g=10m/s2,则小球在空中运动时间及抛出的初速度正确的是( )| A. | t=1.5s | B. | v0=10m/s | C. | t=2s | D. | 5$\sqrt{3}$m/s |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据平行四边形定则求出两个时刻的竖直方向上的分速度与水平速度的关系,结合速度时间公式求出初速度的大小,从而得出落地的竖直分速度,结合速度时间公式求出在空中运动的时间.
解答 解:设物体的初速度为v0,
根据平行四边形定则知,落地前1s时刻的竖直分速度vy1=v0tan30°,
落地时的竖直分速度vy=v0tan60°,
根据vy-vy1=gt1=10m/s,
解得初速度${v}_{0}=5\sqrt{3}m/s$.
则落地时竖直分速度vy=v0tan60°=15m/s,
物体在空中的运动时间t=$\frac{{v}_{y}}{g}=\frac{15}{10}=1.5s$.
故选:AD
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 实验室里的交流发电机可简化为如图所示的模型,正方形线圈在水平匀强磁场中,绕垂直于磁感线的OO′轴匀速转动.今在发电机的输出端接一个电阻R和理想电压表,并让线圈每秒转25圈,读出电压表的示数为10V.已知R=l0Ω,线圈电阻忽略不汁,下列说法正确的是( )
实验室里的交流发电机可简化为如图所示的模型,正方形线圈在水平匀强磁场中,绕垂直于磁感线的OO′轴匀速转动.今在发电机的输出端接一个电阻R和理想电压表,并让线圈每秒转25圈,读出电压表的示数为10V.已知R=l0Ω,线圈电阻忽略不汁,下列说法正确的是( )
 实验室里的交流发电机可简化为如图所示的模型,正方形线圈在水平匀强磁场中,绕垂直于磁感线的OO′轴匀速转动.今在发电机的输出端接一个电阻R和理想电压表,并让线圈每秒转25圈,读出电压表的示数为10V.已知R=l0Ω,线圈电阻忽略不汁,下列说法正确的是( )
实验室里的交流发电机可简化为如图所示的模型,正方形线圈在水平匀强磁场中,绕垂直于磁感线的OO′轴匀速转动.今在发电机的输出端接一个电阻R和理想电压表,并让线圈每秒转25圈,读出电压表的示数为10V.已知R=l0Ω,线圈电阻忽略不汁,下列说法正确的是( )| A. | 从图示位置开始计时线圈中感应电流瞬时值表达式为i=$\sqrt{2}$sin50πtA | |
| B. | 在如图所示的位置时,线圈的磁通量的变化率为零 | |
| C. | 流过电阻R的电流每秒钟方向改变25次 | |
| D. | 电阻R上的热功率等于10W |
11.在万有引力理论发展经历中,提出万有引力定律和测出常量的科学家分别是( )
| A. | 开普勒、卡文迪许 | B. | 牛顿、伽利略 | C. | 牛顿、卡文迪许 | D. | 开普勒、伽利略 |
18.下列物理学史正确的是( )
| A. | 开普勒发现了万有引力定律 | |
| B. | 牛顿发现了万有引力定律,被称为“称量地球的质量”的人 | |
| C. | 万有引力常量是卡文迪许通过实验测量并计算得出的 | |
| D. | 伽利略提出了“日心说”,挡住了太阳,推动了地球 |
13.图中小孩正在荡秋千,在秋千离开最高点向最低点运动的过程中,下列说法中正确的是( )

| A. | 绳子的拉力逐渐增大 | |
| B. | 绳子拉力的大小保持不变 | |
| C. | 小孩经图示位置的加速度可能沿a的方向 | |
| D. | 小孩经图示位置的加速度可能沿b的方向 |
 如图,从倾角为θ=37°的斜面底端的正上方h=1.4m高处正对斜面水平抛出一个物体,已知物体落在斜面上距离斜面底端L=1m处,试求物体被抛出时的速度v0.
如图,从倾角为θ=37°的斜面底端的正上方h=1.4m高处正对斜面水平抛出一个物体,已知物体落在斜面上距离斜面底端L=1m处,试求物体被抛出时的速度v0.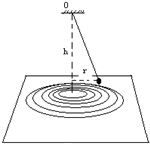 如图所示,是《用圆锥摆粗略验证向心力的表达式》的实验,用手拨动钢球,使它沿纸上的某个圆周运动,该圆周的半径为r,悬点到圆心的距离为h,用秒表记下钢球从第1次到第n次经过圆上某位置所用的总时间t.
如图所示,是《用圆锥摆粗略验证向心力的表达式》的实验,用手拨动钢球,使它沿纸上的某个圆周运动,该圆周的半径为r,悬点到圆心的距离为h,用秒表记下钢球从第1次到第n次经过圆上某位置所用的总时间t. 如图所示,滑块A的质量为m,小车B的质量为M且M=2m,滑块与平板小车之间的动摩擦因数为μ,小车静止在光滑的水平面上,当滑块以速度v0,从小车右端滑上小车,经一段时间后滑块相对小车静止,已知重力加速度为g,求:
如图所示,滑块A的质量为m,小车B的质量为M且M=2m,滑块与平板小车之间的动摩擦因数为μ,小车静止在光滑的水平面上,当滑块以速度v0,从小车右端滑上小车,经一段时间后滑块相对小车静止,已知重力加速度为g,求: 在“研究匀变速直线运动”的实验中,某同学在打出的纸带上按打点的先后顺序每5个点取一个计数点,共取了A、B、C、D、E、F,六个计数点(每相邻两个计数点间还有四个点).从A点开始在每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e段),将这五段纸带由长到短紧靠但不重叠地粘在xoy坐标系中,如图所示.
在“研究匀变速直线运动”的实验中,某同学在打出的纸带上按打点的先后顺序每5个点取一个计数点,共取了A、B、C、D、E、F,六个计数点(每相邻两个计数点间还有四个点).从A点开始在每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e段),将这五段纸带由长到短紧靠但不重叠地粘在xoy坐标系中,如图所示.