题目内容
17．
质量均为m的滑块A、B紧靠着一起从固定斜面顶端由静止开始下滑，它们与斜面之间的摩擦因数分别为μ1和μ2，且μ1＞μ2．在此过程中，物块B对A的压力为（ ）| A． | $\frac{（{μ}_{1}-{μ}_{2}）mgcosθ}{2}$ | B． | （μ1-μ2）mgcosθ | C． | mgsinθ-μ1mgcosθ | D． | 0 |
分析 先以两个物体整体为研究对象，由牛顿第二定律求出加速度，再隔离其中一个物体研究，求出1施于2的作用力大小．
解答 解：整体由牛顿第二定律得：
2mgsinθ-μ1mgcosθ-μ2mgcosθ=2ma
对A由牛顿第二定律得：
F+mgsinθ-μ1mgcosθ=ma
联立解得：F=$\frac{（{μ}_{1}-{μ}_{2}）mgcosθ}{2}$．
故选：A．
点评 本题是连接体问题，考查灵活选择研究对象的能力，往往用整体法求加速度，而求内力时必须用隔离法．
练习册系列答案
相关题目
如图所示，一个圆盘在水平面内匀速转动，角速度是4rad/s，盘面上距盘中心0.10m的位置有一个质量为10g的小物体与圆盘保持静止，跟着圆盘一起做匀速圆周运动．
6．物体1的重力势能Ep1=3J，物体2的重力势能Ep2=-3J，则（ ）
| A． | Ep1=Ep2 | B． | Ep1＞Ep2 | C． | Ep1＜Ep2 | D． | 无法判断 |
5．某同学测定一细金属丝的电阻率，部分实验步骤如下：
（1）用螺旋测微器测量该金属丝的直径，螺旋测微器如图所示，则该金属丝的直径为0.200mm．
（2）因找不到合适的电压表，给同学设计了如图乙所示的电路，电源电动势为E=3V，内阻不能忽略．取金属丝R，接入电路的长度为20cm，接通电路后调整电阻箱的阻值，使电流表示数为0.50A，之后不断改变R，接入电路的长度，调整电阻箱的阻值，使电流表示数始终为0.50A，记录下电阻丝R接入电路的长度及对应电阻箱的阻值如下表所示：
（3）根据图象可求得：该金属丝的电阻率为 ρ=2.0×10-7Ω•m，电源的内阻为r=1.2Ω．（计算结果保留2位有效数字）
（1）用螺旋测微器测量该金属丝的直径，螺旋测微器如图所示，则该金属丝的直径为0.200mm．
（2）因找不到合适的电压表，给同学设计了如图乙所示的电路，电源电动势为E=3V，内阻不能忽略．取金属丝R，接入电路的长度为20cm，接通电路后调整电阻箱的阻值，使电流表示数为0.50A，之后不断改变R，接入电路的长度，调整电阻箱的阻值，使电流表示数始终为0.50A，记录下电阻丝R接入电路的长度及对应电阻箱的阻值如下表所示：
| 长度L（cm） | 10 | 20 | 30 | 40 | 50 | 60 |
| 电阻箱R0（Ω） | 4.2 | 3.5 | 2.3 | 2.2 | 1.5 | 1.0 |
12．
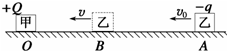如图所示，一个电量为+Q的点电荷甲，固定在绝缘水平面上的O点，另一个电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲滑动，到B点时速度最小且为v．已知静电力常量为k，点电荷乙与水平面的动摩擦因数为μ，AB间距离为L，则以下说法正确的是（ ）
如图所示，一个电量为+Q的点电荷甲，固定在绝缘水平面上的O点，另一个电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲滑动，到B点时速度最小且为v．已知静电力常量为k，点电荷乙与水平面的动摩擦因数为μ，AB间距离为L，则以下说法正确的是（ ）| A． | OB间的距离为 $\sqrt{\frac{kQq}{μmg}}$ | |
| B． | 从开始运动到碰到甲之前的瞬间，乙的加速度逐渐减小 | |
| C． | 从A到B的过程中，电场力对点电荷乙做的功为W=μmgL+$\frac{1}{2}$mv2-$\frac{1}{2}$mv02 | |
| D． | 从A到B的过程中，乙的电势能减少 |
9．
如图所示，面积为0.02m2、内阻不计的100匝矩形线圈ABCD，绕垂直于磁场的轴OO′匀速转动，转动的角速度为100rad/s，匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T．矩形线圈通过滑环与理想变压器相连，触头P可移动，副线圈所接电阻R=50Ω，电表均为理想交流电表．当线圈平面与磁场方向平行时开始计时．下列说法正确的是（ ）
如图所示，面积为0.02m2、内阻不计的100匝矩形线圈ABCD，绕垂直于磁场的轴OO′匀速转动，转动的角速度为100rad/s，匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T．矩形线圈通过滑环与理想变压器相连，触头P可移动，副线圈所接电阻R=50Ω，电表均为理想交流电表．当线圈平面与磁场方向平行时开始计时．下列说法正确的是（ ）| A． | 线圈中感应电动势的表达式为e=100cos（100t）V | |
| B． | P上移时，电流表示数减小 | |
| C． | t=0时，电压表示数为100$\sqrt{2}$V | |
| D． | 当原、副线圈匝数比为2：1时，电阻上消耗的功率为50W |
6．下列说法正确的是（ ）
| A． | 速度的变化量越大，加速度就越大 | |
| B． | 在匀变速直线运动中，速度方向与加速度方向一定相同 | |
| C． | 平抛运动是匀变速曲线运动 | |
| D． | 匀速圆周运动的线速度、角速度、周期都不变 |
如图甲为某探究小组为测定动摩擦因数的设置，水平平台的右端安装有轻质定滑轮，质量为M=2.5kg的物块A放在与滑轮相距L的平台上，现有一轻绳跨过定滑轮，左端与物块连接，右端挂质量为m=0.5kg的小球B，绳拉直时用手托住小球使其在距地面高h处静止，绳与滑轮间的摩擦不计，重力加速度为g（g取10m/s2）．设最大静摩擦力等于滑动摩擦力．由静止释放小球，系统运动，该小组对小球匀加速下落过程拍得同一底片上多次曝光的照片如图（乙）所示，拍摄时每隔1秒曝光一次，若小球直径为20cm，则系统加速度等于0.4m/s2，物块A与平台间的动摩擦因数μ=0.152．