题目内容
 如图所示,ab是水平的光滑轨道,bc是与ab相切的位于竖直平面内、半径R=0.4m的半圆形光滑轨道.现在A、B两个小物体之间夹一个被压缩的弹簧(弹簧未与A、B挂接)后用细线拴住,使其静止在轨道ab上.当烧断细线后,A物体被弹簧弹开,此后它恰能沿半圆形轨道通过其最高点c.已知A和B的质量分别为mA=0.1kg和mB=0.2kg,重力加速度g取10m/s2,所有物体均可视为质点.求:
如图所示,ab是水平的光滑轨道,bc是与ab相切的位于竖直平面内、半径R=0.4m的半圆形光滑轨道.现在A、B两个小物体之间夹一个被压缩的弹簧(弹簧未与A、B挂接)后用细线拴住,使其静止在轨道ab上.当烧断细线后,A物体被弹簧弹开,此后它恰能沿半圆形轨道通过其最高点c.已知A和B的质量分别为mA=0.1kg和mB=0.2kg,重力加速度g取10m/s2,所有物体均可视为质点.求:(1)A在半圆形轨道的最高点c处时的速度大小;
(2)A刚过半圆形轨道最低点b时,对轨道的压力大小;
(3)烧断细线前,弹簧的弹性势能.
分析:(1)能到达半圆形轨道最高点的临界条件是v≥
,恰好能通过最高点说明在最高点重力完全提供向心力,依此求解即可;
(2)根据机械能守恒可以求出小球在b点时的速度,根据圆周运动在最高点和最低点合力提供向心力求解即可;
(3)烧断细线前后,系统满足动能量守恒和机械能守恒,据此求解即可.
| gR |
(2)根据机械能守恒可以求出小球在b点时的速度,根据圆周运动在最高点和最低点合力提供向心力求解即可;
(3)烧断细线前后,系统满足动能量守恒和机械能守恒,据此求解即可.
解答:解:(1)设弹簧弹开后B物体与A物体的速度大小分别为v1和v2,A物体在c点的速度大小为v3.由于A恰能过c点,说明A在c点时对轨道无压力,此时由重力提供向心力由牛顿第二定律有mAg=mA
代入数据解得v3=2m/s(1分)
(2)A从b点到c点的过程中,机械能守恒有
mA
=
mA
+2mAgR
v2=
代入数据解得v2=2
m/s
在b点,轨道对A的支持力F与重力mAg的合力提供向心力
由牛顿第二定律:F-mAg=mA
代入数据解得F=6N
由牛顿第三定律可得A对轨道的压力大小为6N
(3)A、B被弹开的过程中,它们组成的系统动量守恒
有mAv2-mBv1=0
代入数据解得v1=
m/s
该过程中A、B和弹簧组成的系统机械能守恒
有EP=
mA
+
mB
代入数据解得烧断细线前,弹簧的弹性势能EP=1.5J
答:(1)A在半圆形轨道的最高点c处时的速度大小为v3=2m/s;
(2)A刚过半圆形轨道最低点b时,对轨道的压力大小为6N;
(3)烧断细线前,弹簧的弹性势能为1.5J.
| ||
| R |
代入数据解得v3=2m/s(1分)
(2)A从b点到c点的过程中,机械能守恒有
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 3 |
v2=
|
| 5 |
在b点,轨道对A的支持力F与重力mAg的合力提供向心力
由牛顿第二定律:F-mAg=mA
| ||
| R |
代入数据解得F=6N
由牛顿第三定律可得A对轨道的压力大小为6N
(3)A、B被弹开的过程中,它们组成的系统动量守恒
有mAv2-mBv1=0
代入数据解得v1=
| 5 |
该过程中A、B和弹簧组成的系统机械能守恒
有EP=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
代入数据解得烧断细线前,弹簧的弹性势能EP=1.5J
答:(1)A在半圆形轨道的最高点c处时的速度大小为v3=2m/s;
(2)A刚过半圆形轨道最低点b时,对轨道的压力大小为6N;
(3)烧断细线前,弹簧的弹性势能为1.5J.
点评:小球刚好到达圆管形轨道最高点的条件是:到达最高点时速度为零;应用动能定理、牛顿第二定律、能量守恒定律即可正确解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
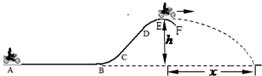 (2012?静安区一模).运动员驾驶摩托车做腾跃特技表演.如图所示,AB是水平路面,长度为L=100m,BCD是一段曲面,AB、BC相切于B点,DEF是一段半径为R=10m的圆弧曲面,E为圆弧的顶点.运动员驾驶摩托车的功率恒定.从A点由静止出发,经过t1=15s到B点,在AB段所受的阻力f=90N,摩托车过B点时速度vB=20m/s,再经t2=2s的时间,摩托车通过圆弧曲面的顶点E,此时压力传感器显示摩托车对E点的压力为零,摩托车通过E后做平抛运动,落地点与E点的水平距离为x=18m.已知人车总质量为m=180kg,重力加速度g=10m/s2.求:
(2012?静安区一模).运动员驾驶摩托车做腾跃特技表演.如图所示,AB是水平路面,长度为L=100m,BCD是一段曲面,AB、BC相切于B点,DEF是一段半径为R=10m的圆弧曲面,E为圆弧的顶点.运动员驾驶摩托车的功率恒定.从A点由静止出发,经过t1=15s到B点,在AB段所受的阻力f=90N,摩托车过B点时速度vB=20m/s,再经t2=2s的时间,摩托车通过圆弧曲面的顶点E,此时压力传感器显示摩托车对E点的压力为零,摩托车通过E后做平抛运动,落地点与E点的水平距离为x=18m.已知人车总质量为m=180kg,重力加速度g=10m/s2.求: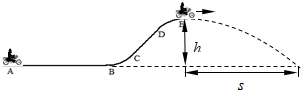
 运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目.如图所示,AB是水平路面,BC是半径为20m的圆弧,CDE是一段曲面.运动员驾驶功率始终为9kW的摩托车,先在AB段加速、经过4.3s到B点时达到最大速度20m/s,再经3s的时间通过坡面到达E点时关闭发动机水平飞出.已知人的质量为60kg、摩托车的质量为120kg,坡顶高度h=5m,落地点与E点的水平距离x=16m,重力加速度g=10m/s2.设摩托车在AB段所受的阻力恒定,运动员及摩托车可看作质点.求:
运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目.如图所示,AB是水平路面,BC是半径为20m的圆弧,CDE是一段曲面.运动员驾驶功率始终为9kW的摩托车,先在AB段加速、经过4.3s到B点时达到最大速度20m/s,再经3s的时间通过坡面到达E点时关闭发动机水平飞出.已知人的质量为60kg、摩托车的质量为120kg,坡顶高度h=5m,落地点与E点的水平距离x=16m,重力加速度g=10m/s2.设摩托车在AB段所受的阻力恒定,运动员及摩托车可看作质点.求: (2011?椒江区模拟)运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目.如图所示,AB是水平路面,长度为L=6m,BC是半径为R=20.75m的圆弧,AB、BC相切于B点,CDE是一段曲面.运动员驾驶功率始终为P=9kW的摩托车,从A点由静止出发,经过t1=4.3s到B点,此时压力传感器显示摩托车对地压力大小为F=3.6×104N.再经t2=3s的时间,摩托车通过坡面到达E点水平飞出.已知人的质量为m=60kg,摩托车的质量为M=120kg,运动员驾驶摩托车行驶时,前后轮着地点连线到整体重心的距离恰为r=0.75m,坡顶高度h=5m,落地点与E点的水平距离x=16m,重力加速度g=10m/s2.求:
(2011?椒江区模拟)运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目.如图所示,AB是水平路面,长度为L=6m,BC是半径为R=20.75m的圆弧,AB、BC相切于B点,CDE是一段曲面.运动员驾驶功率始终为P=9kW的摩托车,从A点由静止出发,经过t1=4.3s到B点,此时压力传感器显示摩托车对地压力大小为F=3.6×104N.再经t2=3s的时间,摩托车通过坡面到达E点水平飞出.已知人的质量为m=60kg,摩托车的质量为M=120kg,运动员驾驶摩托车行驶时,前后轮着地点连线到整体重心的距离恰为r=0.75m,坡顶高度h=5m,落地点与E点的水平距离x=16m,重力加速度g=10m/s2.求: