题目内容
1. 如图所示,足够长的U型光滑导体框架的两个平行导轨间距为L,导轨间连有定值电阻R,框架平面与水平面之间的夹角为θ,不计导体框架的电阻.整个装置处于匀强磁场中,磁场方向垂直于框架平面向上,磁感应强度大小为B.导体棒ab的质量为m,电阻不计,垂直放在导轨上并由静止释放,重力加速度为g,则( )
如图所示,足够长的U型光滑导体框架的两个平行导轨间距为L,导轨间连有定值电阻R,框架平面与水平面之间的夹角为θ,不计导体框架的电阻.整个装置处于匀强磁场中,磁场方向垂直于框架平面向上,磁感应强度大小为B.导体棒ab的质量为m,电阻不计,垂直放在导轨上并由静止释放,重力加速度为g,则( )| A. | 导体棒b端的电势高于a | |
| B. | 当导体棒达到最大速度v,ab所受安培力为$\frac{{B}^{2}{L}^{2}V}{R}$sinθ | |
| C. | 导体棒的最大速度为$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$ | |
| D. | 整个加速过程中的平均速度大于$\frac{mgRsinθ}{2{B}^{2}{L}^{2}}$ |
分析 根据右手定则判断电势的高低.当导体棒达到最大速度时做匀速运动,根据平衡条件和安培力公式F安=$\frac{{B}^{2}{L}^{2}v}{R}$求解最大速度.导体棒做加速度减小的变加速运动,结合匀变速运动的平均速度公式$\overline{v}$=$\frac{{v}_{0}+v}{2}$分析D项.
解答 解:A、根据右手定则知,ab中感应电流方向由b→a,a相当于电源正极,电势较高,故A错误.
B、当导体棒达到最大速度v,感应电动势为 E=BLv,感应电流为 I=$\frac{E}{R}$,ab所受的安培力大小为 F安=BIL,联立解得F安=$\frac{{B}^{2}{L}^{2}v}{R}$,故B错误.
C、当导体棒达到最大速度时做匀速运动,根据平衡条件得:mgsinθ=F安=$\frac{{B}^{2}{L}^{2}v}{R}$,可得 v=$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$,故C正确.
D、若导体棒做匀加速运动时,平均速度等于$\frac{v}{2}$=$\frac{mgRsinθ}{2{B}^{2}{L}^{2}}$,而实际上导体棒做加速度减小的变加速运动,由v-t图象知,变加速运动的位移大于匀加速运动的位移,平均平均速度也大于匀加速运动的平均速度,所以整个加速过程中的平均速度大于$\frac{mgRsinθ}{2{B}^{2}{L}^{2}}$,故D正确.
故选:CD.
点评 解决本题的关键要明确导体棒的运动过程,再对金属棒正确受力分析,应用安培力公式、功率公式和平衡条件等知识,即可正确解答.

练习册系列答案
相关题目
11.下列叙述中符合物理学史实的是( )
| A. | 麦克斯韦预言了电磁波,奥斯特发现了电磁感应现象 | |
| B. | 伽利略通过斜面理想实验得出了维持运动不需要力的结论 | |
| C. | 库仑通过对电荷间相互作用的研究提出了库仑定律,并测定了元电荷的数值 | |
| D. | 牛顿发现了行星的运动规律,总结出了万有引力定律,并计算出引力常量G的值 |
12.一些星球由于某种原因而发生收缩,假设该星球的直径变为原来的四分之一,若收缩时质量不变,则与收缩前相比( )
| A. | 同一物体在星球表面受到的重力增大到原来的4倍 | |
| B. | 同一物体在星球表面受到的重力增大到原来的16倍 | |
| C. | 星球的第一宇宙速度增大到原来的4倍 | |
| D. | 星球的第一宇宙速度增大到原来的2倍 |
16.有下列几种情景,请根据所学知识选择对情景的分析和判断正确的说法( )
①点火后即将升空的火箭
②高速公路上沿直线高速行驶的轿车为避免事故紧急刹车
③运行的磁悬浮列车在轨道上高速行驶
④太空的空间站在绕地球匀速转动.
①点火后即将升空的火箭
②高速公路上沿直线高速行驶的轿车为避免事故紧急刹车
③运行的磁悬浮列车在轨道上高速行驶
④太空的空间站在绕地球匀速转动.
| A. | 因火箭还没运动,所以加速度一定为零 | |
| B. | 轿车紧急刹车,速度变化很快,所以加速度很大 | |
| C. | 高速行驶的磁悬浮列车,因速度很大,所以加速度也一定很大 | |
| D. | 因为空间站绕地球匀速转动,所以加速度为零 |
13.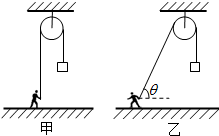 如图所示,某人通过定滑轮将一重物提升.第一次,此人竖直向下拉绳(甲图),使物体匀速上升高度h,该过程人对物体做功为W.第二次,此人拉着绳从定滑轮正下方以速度v匀速向左运动(乙图),使物体上升相同的高度,此时绳子与水平方向的夹角为θ,已知重力加速度为g.则第二次人对物体做的功为( )
如图所示,某人通过定滑轮将一重物提升.第一次,此人竖直向下拉绳(甲图),使物体匀速上升高度h,该过程人对物体做功为W.第二次,此人拉着绳从定滑轮正下方以速度v匀速向左运动(乙图),使物体上升相同的高度,此时绳子与水平方向的夹角为θ,已知重力加速度为g.则第二次人对物体做的功为( )
 如图所示,某人通过定滑轮将一重物提升.第一次,此人竖直向下拉绳(甲图),使物体匀速上升高度h,该过程人对物体做功为W.第二次,此人拉着绳从定滑轮正下方以速度v匀速向左运动(乙图),使物体上升相同的高度,此时绳子与水平方向的夹角为θ,已知重力加速度为g.则第二次人对物体做的功为( )
如图所示,某人通过定滑轮将一重物提升.第一次,此人竖直向下拉绳(甲图),使物体匀速上升高度h,该过程人对物体做功为W.第二次,此人拉着绳从定滑轮正下方以速度v匀速向左运动(乙图),使物体上升相同的高度,此时绳子与水平方向的夹角为θ,已知重力加速度为g.则第二次人对物体做的功为( )| A. | W+$\frac{{W{v^2}{{sin}^2}θ}}{2gh}$ | B. | W+$\frac{{W{v^2}{{cos}^2}θ}}{2gh}$ | C. | W | D. | W-$\frac{{W{v^2}{{cos}^2}θ}}{2gh}$ |
11.某同学通过以下步骤测出了从一定高度落下的排球对地面的最大冲击力:将一张白纸铺在水平地面上,把排球在水里弄湿,然后让排球从规定的高度自由落下,并在白纸上留下球的水印.再将印有水印的白纸铺在台秤上,将球放在纸上的水印中心,缓慢地向下压球,使排球与纸接触部分逐渐发生形变直至刚好遮住水印,记下此时台秤的示数,即为冲击力最大值.下列物理学习或研究中用到的方法与该同学的方法相同的是( )
| A. | 研究加速度与合力、质量的关系 | B. | 建立“点电荷”的概念 | ||
| C. | 建立“瞬时速度”的概念 | D. | 建立“合力与分力”的概念 |


 如图所示,内径均匀的U型玻璃管竖直放置,管右侧上端封闭,左侧上端开口,内有用细线栓住的活塞.两管中分别封人L=11cm的空气柱A和B,活塞上、下气体压强均等于76cm水银柱产生的压强,这时两管内的水银面的高度差h=6cm,现将活塞用细线缓慢地向上拉,使两管内水银面相平.求活塞向上移动的距离是多少?
如图所示,内径均匀的U型玻璃管竖直放置,管右侧上端封闭,左侧上端开口,内有用细线栓住的活塞.两管中分别封人L=11cm的空气柱A和B,活塞上、下气体压强均等于76cm水银柱产生的压强,这时两管内的水银面的高度差h=6cm,现将活塞用细线缓慢地向上拉,使两管内水银面相平.求活塞向上移动的距离是多少?