题目内容
3.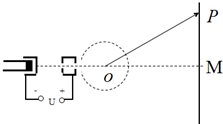 电视机显像管中,电子束的偏转是用磁偏转技术实现.电子束经过电压为U的加速电场后,进入圆形的匀强磁场区,如图12所示,磁场方向垂直于圆面,磁场区的中心为O,半径为r,当不加磁场时,电子束将通过O点而打到屏幕的中心M点.在圆形区域内加垂直圆面、磁感应强度为B的匀强磁场后,电子将打到光屏的上端P点.已知OM=4r,电子的电荷量e,质量为m,不计电子从阴极放出的速度大小,不计空气阻力.求:
电视机显像管中,电子束的偏转是用磁偏转技术实现.电子束经过电压为U的加速电场后,进入圆形的匀强磁场区,如图12所示,磁场方向垂直于圆面,磁场区的中心为O,半径为r,当不加磁场时,电子束将通过O点而打到屏幕的中心M点.在圆形区域内加垂直圆面、磁感应强度为B的匀强磁场后,电子将打到光屏的上端P点.已知OM=4r,电子的电荷量e,质量为m,不计电子从阴极放出的速度大小,不计空气阻力.求:(1)电子打到荧光屏上P点的动能;
(2)电子在磁场中做圆周运动的半径;
(3)P点距M点的距离.
分析 (1)电子在加速电场中做加速运动,电子在磁场中做匀速圆周运动,离开磁场后,电阻做匀速直线运动,整个过程只有电场力做功,应用动能定理可以求出电子的动能.
(2)电子在磁场中做匀速圆周运动,由牛顿第二定律求出电子的轨道半径.
(3)电子离开偏转磁场后做匀速直线运动,应用匀速运动规律与几何知识求出关系式
解答  解:(1)在整个过程中,由动能定理得:eU=$\frac{1}{2}$mv2-0,
解:(1)在整个过程中,由动能定理得:eU=$\frac{1}{2}$mv2-0,
电阻打在荧光屏上的动能:EK=$\frac{1}{2}$mv2=eU;
(2)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:evB=m$\frac{{v}^{2}}{R}$,
解得:R=$\frac{1}{B}$$\sqrt{\frac{2mU}{e}}$;
(3)电子离开偏转磁场时:tan$\frac{θ}{2}$=$\frac{r}{R}$,
由几何知识得:PM=OM•tanθ=4rtanθ,
已知:tanθ=$\frac{2tan\frac{θ}{2}}{1-(tan\frac{θ}{2})^{2}}$
解得:PM=$\frac{8B{r}^{2}\sqrt{2meU}}{2mU-e{B}^{2}{r}^{2}}$;
答:(1)电子打到荧光屏上P点的动能为eU;
(2)电子在磁场中做圆周运动的半径为$\frac{1}{B}$$\sqrt{\frac{2mU}{e}}$;
(3)P点距M点的距离为$\frac{8B{r}^{2}\sqrt{2meU}}{2mU-e{B}^{2}{r}^{2}}$.
点评 本题考查了电子在电场与磁场中的运动,分析清楚电子的运动过程、应用动能定理、牛顿第二定律即可正确解题,解题时注意几何知识的应用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
14.某人造卫星运动的轨道可近似看作是以地心为中心的圆.由于阻力作用,该卫星到地心的距离从r1慢慢变到r2,用v1、v2;EK1、EK2;T1、T2;a1、a2分别表示卫星在这两个轨道上的速度、动能、周期和向心加速度,则( )
| A. | v1>v2 | B. | EK1<EK2 | C. | T1>T2 | D. | a1<a2 |
8. 汤姆逊通过对阴极射线的研究发现了电子,如图所示,阴极射线管的两极分别接在直流高压电源两端,把电子射线管放在蹄形磁铁的两极之间,可以观察荧光屏上的电子运动的轨迹偏转方向是( )
汤姆逊通过对阴极射线的研究发现了电子,如图所示,阴极射线管的两极分别接在直流高压电源两端,把电子射线管放在蹄形磁铁的两极之间,可以观察荧光屏上的电子运动的轨迹偏转方向是( )
 汤姆逊通过对阴极射线的研究发现了电子,如图所示,阴极射线管的两极分别接在直流高压电源两端,把电子射线管放在蹄形磁铁的两极之间,可以观察荧光屏上的电子运动的轨迹偏转方向是( )
汤姆逊通过对阴极射线的研究发现了电子,如图所示,阴极射线管的两极分别接在直流高压电源两端,把电子射线管放在蹄形磁铁的两极之间,可以观察荧光屏上的电子运动的轨迹偏转方向是( )| A. | 向左 | B. | 向右 | C. | 向上 | D. | 向下 |
15. 如图所示,长为2L的直导线折成边长相等,夹角为60°的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为B,当在导线中通以电流I时,该V形通电导线受到的安培力大小为 ( )
如图所示,长为2L的直导线折成边长相等,夹角为60°的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为B,当在导线中通以电流I时,该V形通电导线受到的安培力大小为 ( )
 如图所示,长为2L的直导线折成边长相等,夹角为60°的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为B,当在导线中通以电流I时,该V形通电导线受到的安培力大小为 ( )
如图所示,长为2L的直导线折成边长相等,夹角为60°的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为B,当在导线中通以电流I时,该V形通电导线受到的安培力大小为 ( )| A. | 2BIL | B. | BIL | C. | 0.5BIL | D. | 0 |
12.一列简谐横波沿x轴传播,t=0时刻的波形如图甲所示,A、P和Q是介质中的三个质点,A的振动图象如图乙所示.下列判断正确的是( )


| A. | 该波的传播速度是2.5m/s | |
| B. | 该波沿x轴正方向传播 | |
| C. | 从0~0.4s,P通过的路程为4m | |
| D. | 从t=0时刻开始,P将比Q先回到平衡位置 |
 如图所示,光滑绝缘水平面的右侧有一竖直向下且范围足够大的有界匀强磁场,直线PQ为其边界,矩形闭合线框abcd在水平恒力F作用下从静止开始运动.用t1、t2分别表示ab边和cd边刚进入磁场的时刻,线框运动过程中形状不变,ab边始终保持与PQ平行,不计空气的影响.下列图象能够反映线框运动过程中速度v,随时间t变化规律的是( )
如图所示,光滑绝缘水平面的右侧有一竖直向下且范围足够大的有界匀强磁场,直线PQ为其边界,矩形闭合线框abcd在水平恒力F作用下从静止开始运动.用t1、t2分别表示ab边和cd边刚进入磁场的时刻,线框运动过程中形状不变,ab边始终保持与PQ平行,不计空气的影响.下列图象能够反映线框运动过程中速度v,随时间t变化规律的是( )



 如图,水平粗糙轨道AB与半圆形光滑的竖直圆轨道BC相连,B点与C点的连线沿竖直方向,AB段长为L,圆轨道的半径为R.一个小滑块以初速度vo从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力.求:
如图,水平粗糙轨道AB与半圆形光滑的竖直圆轨道BC相连,B点与C点的连线沿竖直方向,AB段长为L,圆轨道的半径为R.一个小滑块以初速度vo从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力.求: