题目内容
14.某人造卫星运动的轨道可近似看作是以地心为中心的圆.由于阻力作用,该卫星到地心的距离从r1慢慢变到r2,用v1、v2;EK1、EK2;T1、T2;a1、a2分别表示卫星在这两个轨道上的速度、动能、周期和向心加速度,则( )| A. | v1>v2 | B. | EK1<EK2 | C. | T1>T2 | D. | a1<a2 |
分析 人造地球卫星在绕地球做圆周运动时地球对卫星的引力提供圆周运动的向心力列出表示出线速度、加速度和周期等式求解
解答 解:根据万有引力提供向心力有:$G\frac{Mm}{{r}^{2}}$=$m\frac{{v}^{2}}{r}$=m$\frac{4{π}^{2}r}{{T}^{2}}$=ma
v=$\sqrt{\frac{GM}{r}}$
T=2$π\sqrt{\frac{{r}^{3}}{GM}}$
a=$\frac{GM}{{r}^{2}}$
该卫星到地心的距离从r1慢慢减小到r2,
A、B、该卫星到地心的距离从r1慢慢减小到r2,
v1<v2,EKl<EK2,故A错误,B正确
C、该卫星到地心的距离从r1慢慢减小到r2,
T1>T2,故C正确
D、该卫星到地心的距离从r1慢慢减小到r2,
a1<a2,故D正确
故选:BCD
点评 一个天体绕中心天体做圆周运动时万有引力提供向心力,灵活的选择向心力的表达式是我们顺利解决此类题目的基础.我们要按照不同的要求选择不同的公式来进行求解

练习册系列答案
相关题目
19.下面器件中,利用电磁感应原理工作的是( )
| A. | 电吹风机 | B. | 示波管 | C. | 电磁炉 | D. | 质谱仪 |
6. 反氢原子是由一个反质子和一个围绕它运动的正电子组成,反质子和质子有相同的质量,带有等量异种电荷,反氢原子和氢原子相同的能级分布,氢原子能级图如图所示.下列说法正确的是( )
反氢原子是由一个反质子和一个围绕它运动的正电子组成,反质子和质子有相同的质量,带有等量异种电荷,反氢原子和氢原子相同的能级分布,氢原子能级图如图所示.下列说法正确的是( )
 反氢原子是由一个反质子和一个围绕它运动的正电子组成,反质子和质子有相同的质量,带有等量异种电荷,反氢原子和氢原子相同的能级分布,氢原子能级图如图所示.下列说法正确的是( )
反氢原子是由一个反质子和一个围绕它运动的正电子组成,反质子和质子有相同的质量,带有等量异种电荷,反氢原子和氢原子相同的能级分布,氢原子能级图如图所示.下列说法正确的是( )| A. | 反氢原子与氢原子的电离能不相同 | |
| B. | 基态反氢原子能够吸收11eV的光子并发生跃迁 | |
| C. | 反氢原子吸收光子跃迁后,其核外电子的动能变小 | |
| D. | 一个处于n=3能级的反氢原子跃迁时最多能辐射3种不同频率的光 |
 在垂直纸面向外、磁感应强度为B=1T的匀强磁场中,建立如图所示的竖直直角坐标系xOy,在x<0的区域内有沿x轴负向的匀强电场,场强大小为E=$\sqrt{3}$V/m,在x>0的区域也存在匀强电场(图中未画出).一个带正电油滴从x轴上的N点竖直向下做匀速圆周运动至P点后进入x<0的区域,沿着与水平方向成α=30°角斜向上做直线运动,通过x轴上的M点,已知重力加速度为g=10m/s2,求:
在垂直纸面向外、磁感应强度为B=1T的匀强磁场中,建立如图所示的竖直直角坐标系xOy,在x<0的区域内有沿x轴负向的匀强电场,场强大小为E=$\sqrt{3}$V/m,在x>0的区域也存在匀强电场(图中未画出).一个带正电油滴从x轴上的N点竖直向下做匀速圆周运动至P点后进入x<0的区域,沿着与水平方向成α=30°角斜向上做直线运动,通过x轴上的M点,已知重力加速度为g=10m/s2,求: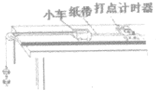 小明把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引力下运动,以此研究绳拉力做功和小车动能变化的关系.此外他还准备了打点计时器及配套电源、导线、复写纸、纸带、小木块、天平(包括砝码)等,实验装置如图
小明把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引力下运动,以此研究绳拉力做功和小车动能变化的关系.此外他还准备了打点计时器及配套电源、导线、复写纸、纸带、小木块、天平(包括砝码)等,实验装置如图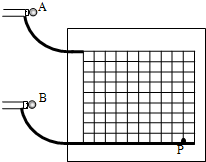 如图所示,在竖直板上不同高度处各固定两个完全相同的圆弧轨道,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断开开关,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一个光滑的水平轨道,则:
如图所示,在竖直板上不同高度处各固定两个完全相同的圆弧轨道,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断开开关,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一个光滑的水平轨道,则: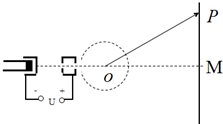 电视机显像管中,电子束的偏转是用磁偏转技术实现.电子束经过电压为U的加速电场后,进入圆形的匀强磁场区,如图12所示,磁场方向垂直于圆面,磁场区的中心为O,半径为r,当不加磁场时,电子束将通过O点而打到屏幕的中心M点.在圆形区域内加垂直圆面、磁感应强度为B的匀强磁场后,电子将打到光屏的上端P点.已知OM=4r,电子的电荷量e,质量为m,不计电子从阴极放出的速度大小,不计空气阻力.求:
电视机显像管中,电子束的偏转是用磁偏转技术实现.电子束经过电压为U的加速电场后,进入圆形的匀强磁场区,如图12所示,磁场方向垂直于圆面,磁场区的中心为O,半径为r,当不加磁场时,电子束将通过O点而打到屏幕的中心M点.在圆形区域内加垂直圆面、磁感应强度为B的匀强磁场后,电子将打到光屏的上端P点.已知OM=4r,电子的电荷量e,质量为m,不计电子从阴极放出的速度大小,不计空气阻力.求: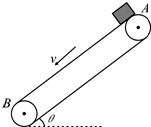 如图所示,一个与水平方向成θ=37°的传送带逆时针转动,线速度为v=10m/s,传送带A、B两轮间距离L=10.25m.一个质量m=1kg的可视为质点的物体轻放在A处,物体与传送带之间的动摩擦因数μ=0.5.sin37°=0.6,cos37°=0.8,g=10m/s2.求:
如图所示,一个与水平方向成θ=37°的传送带逆时针转动,线速度为v=10m/s,传送带A、B两轮间距离L=10.25m.一个质量m=1kg的可视为质点的物体轻放在A处,物体与传送带之间的动摩擦因数μ=0.5.sin37°=0.6,cos37°=0.8,g=10m/s2.求: