题目内容
1.如图所示,设AB段是距水平传送带装置高为H=1.25m的光滑斜面,水平段BC使用水平传送带装置,BC长L=5m,与货物包的动摩擦因数为μ=0.4,皮带轮的半径为R1=0.2m,转动的角度为ω=15rad/s.设质量为m=1kg的小物块由静止开始从A点下滑,经过B点的拐角处无机械能损失.小物块随传送带运动到C点后水平抛出,恰好无碰撞地沿圆弧切线从D点进入竖直光滑圆弧轨道下滑.D、E为圆弧的两端点,其连线水平.已知圆弧半径R2=1.0m圆弧对应圆心角θ=106°,O为轨道的最低点.(g=10m/s2,sin37°=0.6,cos37°=0.8)试求:
(1)小物块在水平传送带BC上的运动时间;
(2)水平传送带上表面距地面的高度;
(3)小物块经过O点时对轨道的压力.
分析 (1)加速下滑过程中只有重力做功,对滑块沿斜面下滑过程运用动能定理列式求解B点速度;小滑块在传送带上先加速后匀速,先受力分析后根据牛顿第二定律求出加速过程的加速度,然后根据速度时间公式求加速时间,再根据平均速度公式求加速位移,再求匀速时间,最后得到总时间;
(2)对于平抛运动,根据速度方向先求出落地时的竖直分速度,然后根据速度位移公式求解出传送带上表面距离地面的高度差;
(3)先根据速度分解的平行四边形定则求出落地时速度,再对从D到O过程运用动能定理列式求出O点速度,最后运用牛顿第二定律求解对轨道最低点压力.
解答 解:(1)小物块由A运动B,由动能定理,有:
mgH=$\frac{1}{2}$mv2
解得:vB=$\sqrt{2gH}$=$\sqrt{2×10×1.25}$=5m/s
在传送带滑动过程,由牛顿第二定律,得:
μmg=ma,
解得:a=μg=4m/s2
水平传送带的速度为v0=R1ω=3m/s
加速过程,由 v0=vB-at1,得:
t1=$\frac{{v}_{B}-{v}_{0}}{a}$=$\frac{5-3}{4}$=0.5s
则匀速过程
L1=$\frac{{v}_{B}+{v}_{0}}{2}$t1=$\frac{5+3}{2}×0.5$=2m
t2=$\frac{L-{L}_{1}}{{v}_{0}}$=$\frac{5-2}{3}$=1s
故总时间:
t=t1+t2=1.5s
(2)小物块从C到D做平抛运动,在D点有:
vy=v0tan$\frac{θ}{2}$=3×$\frac{4}{3}$=4m/s
由${v}_{y}^{2}$=2gh,得h=$\frac{{v}_{y}^{2}}{2g}$=$\frac{16}{20}$=0.8m
(3)小物块在D点的速度大小为:
vD=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5m/s
对小物块从D点到O由动能定理,得:
mgR(1-cos$\frac{θ}{2}$)=$\frac{1}{2}$mv2-$\frac{1}{2}$m${v}_{D}^{2}$
在O点,由牛顿第二定律,得:
FN-mg=m$\frac{{v}^{2}}{R}$
联立以上两式解得:FN=43N
由牛顿第三定律知对轨道的压力为:FN′=43N
答:(1)小物块在水平传送带BC上的运动时间为1.5s;
(2)水平传送带上表面距地面的高度为0.8m;
(3)小物块经过O点时对轨道的压力为43N.
点评 本题关键是分析清楚物体的运动情况,然后根据动能定理、平抛运动知识、牛顿第二定律、向心力公式列式求解.

| A. |  如图说明分子间存在引力 | |
| B. |  如图在用油膜法测分子大小时,多撒痱子粉比少撒好 | |
| C. |  如图说明,气体压强的大小既与分子动能有关,也与分子的密集程度有关 | |
| D. |  如图水黾停在水面上的原因是水黾受到了水的浮力作用 |
| A. | 能量的概念是牛顿首先提出的一个力学概念 | |
| B. | 能量的概念是伽利略提出的,并用斜面理想实验来验证能量的存在 | |
| C. | 人们从伽利略的斜面实验得到启发,认识到引入能量概念的重要性 | |
| D. | 以上说法都不正确 |
 如图所示,质量相同的两物体与水平面的动摩擦因数相同,分别用大小相等与水平夹角相同的力F1和F2作用在物体上,使物体均能在水平面内由静止开始做匀加速直线运动,甲图中F1为拉力,乙图中F2为推力,当两物体经相同位移运动时,F1和F2对物体做的功分别为W1和W2,做功平均功率为P1和P2,物体加速度为a1和a2,则( )
如图所示,质量相同的两物体与水平面的动摩擦因数相同,分别用大小相等与水平夹角相同的力F1和F2作用在物体上,使物体均能在水平面内由静止开始做匀加速直线运动,甲图中F1为拉力,乙图中F2为推力,当两物体经相同位移运动时,F1和F2对物体做的功分别为W1和W2,做功平均功率为P1和P2,物体加速度为a1和a2,则( )| A. | W1>W2 P1>P2 | B. | W1=W2 P1>P2 | C. | P1>P2 a1>a2 | D. | a1=a2 P1=P2 |
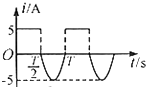 如图所示为一交变电流的i-t图象,其中每个周期的后半周期的图象为半个周期的正弦曲线,则该交变电流的有效值是( )
如图所示为一交变电流的i-t图象,其中每个周期的后半周期的图象为半个周期的正弦曲线,则该交变电流的有效值是( )| A. | $\frac{5\sqrt{3}}{2}$A | B. | 5A | C. | 10A | D. | 0A |
 根据α粒子散射实验,卢瑟福提出了原子的核式结构模型.图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动轨迹,在α粒子从a运动到b,再运动到c的过程中,下列说法中正确的是( )
根据α粒子散射实验,卢瑟福提出了原子的核式结构模型.图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动轨迹,在α粒子从a运动到b,再运动到c的过程中,下列说法中正确的是( )| A. | 动能先增大,后减小 | |
| B. | 电势能选减小,后增大 | |
| C. | 电场力先做负功,后做正功,总功为零 | |
| D. | 加速度先变大,后变小 |
 如图甲所示,固定在水平桌面上的光滑金属导轨cd、eg处于方向垂直导轨向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点C、e之间连接一电阻,其他部分电阻忽略不计.现用一水平向右的外力F1作用在金属杆ab上,使金属杆ab向右沿导轨滑动,滑动过程中金属杆ab始终垂直于导轨.金属杆ab受到的安培力用F2表示,F1与F2随时间t变化的关系图象如图乙所示,下面关于金属杆ab运动过程中的v-t图象不正确的是( )
如图甲所示,固定在水平桌面上的光滑金属导轨cd、eg处于方向垂直导轨向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点C、e之间连接一电阻,其他部分电阻忽略不计.现用一水平向右的外力F1作用在金属杆ab上,使金属杆ab向右沿导轨滑动,滑动过程中金属杆ab始终垂直于导轨.金属杆ab受到的安培力用F2表示,F1与F2随时间t变化的关系图象如图乙所示,下面关于金属杆ab运动过程中的v-t图象不正确的是( )



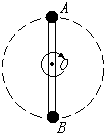 如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m?,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.
如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m?,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动. ①将条形磁铁按图所示方向插入闭合线圈.在磁铁插入的过程中,灵敏电流表示数不为零.
①将条形磁铁按图所示方向插入闭合线圈.在磁铁插入的过程中,灵敏电流表示数不为零.