题目内容
9. 如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁场的磁感应强度为B.在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计).则下列说法正确的是( )
如图所示,在x轴上方存在垂直于纸面向里的匀强磁场,磁场的磁感应强度为B.在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计).则下列说法正确的是( )| A. | 若v一定,θ越大,则粒子离开磁场的位置距O点越远 | |
| B. | 若v一定,θ越大,则粒子在磁场中运动的时间越短 | |
| C. | 若θ一定,v越大,则粒子在磁场中运动的角速度越大 | |
| D. | 若θ一定,v越大,则粒子在磁场中运动的时间越短 |
分析 带电粒子进入磁场中,受到洛伦兹力而做匀速圆周运动,作出轨迹,由轨迹对应的圆心角等于粒子速度的偏向角,求出轨迹的圆心角α,由t=$\frac{α}{2π}T$分析时间.
根据几何知识分析粒子离开磁场的位置与半径的关系;由ω=$\frac{2π}{T}$,$T=\frac{2πm}{qB}$分析角速度.
解答 解:A、设粒子的轨迹半径为r,则r=$\frac{mv}{qB}$.如图,AO=2rsinθ=$\frac{2mvsinθ}{qB}$,则若θ是锐角,θ越大,AO越大.若θ是钝角,θ越大,AO越小. 故A错误.
故A错误.
B、如图,画出粒子在磁场中运动的轨迹.由几何关系得:轨迹对应的圆心角α=2π-2θ
粒子在磁场中运动的时间t=$\frac{α}{2π}T$=$\frac{2π-2θ}{2π}•\frac{2πm}{qB}$=$\frac{(2π-2θ)m}{qB}$,则得知:若v一定,θ越大,时间t越短;若θ一定,运动时间一定.
故B正确,D错误.
C、粒子在磁场中运动的角速度ω=$\frac{2π}{T}$,又T=$\frac{2πm}{qB}$,则得ω=$\frac{qB}{m}$,与速度v无关.故C错误.
故选:B.
点评 带电粒子在匀强磁场中做匀速圆周运动的时间,常常根据t=$\frac{θ}{2π}$T,θ是轨迹的圆心角,根据几何知识,轨迹的圆心角等于速度的偏向角.

练习册系列答案
相关题目
19.张帅摇动苹果树,从同一高度一个苹果和一片树叶同时从静止直接落到地上,苹果先着地,下面说法中正确的是( )
| A. | 苹果和树叶做的都是自由落体运动 | |
| B. | 苹果和树叶的运动加速度都是重力加速度 | |
| C. | 假如地球上没有空气,则苹果和树叶会同时落地 | |
| D. | 以上说法都不对 |
20.在探究波的形成过程中,某同学将一根足够长的绳子一端固定在竖直墙壁上,用手捏住绳子的另一端上下振动,形成了沿水平面方向传播的波,波的传播速度为v,周期为T.经过一段时间后,该波传播到某质点A.若此波可视为简谐横波且传播过程中不计能量损失.关于这列波及质点A的振动,下列说法正确的是( )
| A. | 质点A振动的周期一定为T | |
| B. | 质点A振动的平均速度就是该波的传播速度 | |
| C. | 这列波的传播速度与手捏绳子振动的振幅无关 | |
| D. | 质点A开始振动后,经过时间t,质点A沿传播方向移动的距离为vt | |
| E. | 若质点A与手捏点的距离是vT,则质点A振动时与手捏点的振动位移总是相同 |
4.下列叙述中正确的是( )
| A. | 康普顿预言了中子的存在 | |
| B. | 在α粒子散射实验的基础上,卢瑟福提出了原子的核式结构模型 | |
| C. | 氡的半衰期为3.8天,若取4个氡原子核,经过7.6天后就一定只剩下一个氡原子核 | |
| D. | 一群处于n=4能级的氢原子回到n=2状态过程中,可能辐射3种不同频率的光子 |
18. 矩形线框在匀强磁场内绕垂直与磁场的轴匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场内绕垂直与磁场的轴匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
 矩形线框在匀强磁场内绕垂直与磁场的轴匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场内绕垂直与磁场的轴匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )| A. | 该交流电的电压瞬时值的表达式为u=36$\sqrt{2}$sin0.5πt(V) | |
| B. | 交流电压的最小值为-36$\sqrt{2}$V,频率为25Hz | |
| C. | t=0时,相框平面与中性面重合 | |
| D. | 1s末线框平面平行于磁场,通过线框的磁通量变化最快 |


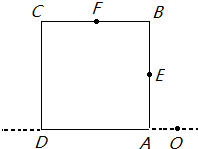 如图所示,空气中一透明柱体的横截面是边长为d的正方形ABCD,在DA边的延长线上距A点$\frac{{\sqrt{3}}}{6}d$处有一点光源O,发出一束单色光从AB边中点E进入介质后,经BC中点F射出,求:
如图所示,空气中一透明柱体的横截面是边长为d的正方形ABCD,在DA边的延长线上距A点$\frac{{\sqrt{3}}}{6}d$处有一点光源O,发出一束单色光从AB边中点E进入介质后,经BC中点F射出,求: 如图为一列沿x轴传播的简谐横波在t1=0(图中实线所示)以及在t2=0.02s(虚线所示)两个时刻的波形图象.
如图为一列沿x轴传播的简谐横波在t1=0(图中实线所示)以及在t2=0.02s(虚线所示)两个时刻的波形图象.