题目内容
19. 设在地面上方的真空室内,存在着方向水平向右的匀强电场和方向垂直于纸面向内的匀强磁场,如图所示.一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,O、A连线在竖直方向上,AC弧对应的圆心角θ=37°,今有一质量m=3.6×10-4kg、电荷量q=+9.0×10-4C的带电小球,以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,此后小球做匀速直线运动.重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8 求:
设在地面上方的真空室内,存在着方向水平向右的匀强电场和方向垂直于纸面向内的匀强磁场,如图所示.一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,O、A连线在竖直方向上,AC弧对应的圆心角θ=37°,今有一质量m=3.6×10-4kg、电荷量q=+9.0×10-4C的带电小球,以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,此后小球做匀速直线运动.重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8 求:(1)匀强电场的场强E.
(2)小球射入圆弧轨道后的瞬间,小球对轨道的压力.
分析 (1)根据小球离开C点时处于平衡状态列平衡方程可正确求解;
(2)根据动能定理求出小球刚进入磁场时的速度大小,从而进一步求出磁场强度,在最低点进行受力分析,根据向心力公式列方程可正确求解.
解答 解:(1)当小球离开圆弧轨道后,对其受力分析如图所示: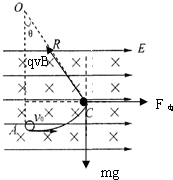
由平衡条件得:F电=qE=mgtanθ
代入数据解得:E=3N/C
(2)小球从进入圆弧轨道到离开圆弧轨道的过程中,由动能定理得:
F电Rsinθ-mgR(1-cosθ)=$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
代入数据得:v=5m/s
由F磁=qvB=$\frac{mg}{cosθ}$
解得:B=1T
分析小球射入圆弧轨道瞬间的受力情况如图所示:
由牛顿第二定律得:FN+Bqvo-mg=$m\frac{{v}_{0}^{2}}{R}$
代入数据得:FN=3.2×10-3 N
由牛顿第三定律得,小球对轨道的压力为:FN=3.2×10-3 N
答:(1)匀强电场的场强为3N/C;
(2)小球射入圆弧轨道后的瞬间对轨道的压力为3.2×10-3 N.
点评 本题考查了带电粒子在复合场中的运动,对于这类问题关键是正确进行受力分力,明确运动形式,根据相关规律解答.

练习册系列答案
相关题目
12. 下面是在某星球上“用单摆测定重力速度”的实验中获得的有关数据:
下面是在某星球上“用单摆测定重力速度”的实验中获得的有关数据:
(1)利用上述数据在图所示的坐标中作出l-T2图象.
(2)利用图象,取T2=0.1×4π2=3.95s2,求出重力加速度的值.
 下面是在某星球上“用单摆测定重力速度”的实验中获得的有关数据:
下面是在某星球上“用单摆测定重力速度”的实验中获得的有关数据:| 摆长l/m | 0.5 | 0.6 | 0.8 | 1.1 |
| 周期T2/s2 | 2.0 | 2.5 | 3.2 | 4.5 |
(2)利用图象,取T2=0.1×4π2=3.95s2,求出重力加速度的值.
13.以下说法哪些是正确的( )
| A. | 当光的波长比圆孔直径小时,可产生明显的衍射现象 | |
| B. | 衍射现象的研究表明,光沿直线传播只是一种近似规律 | |
| C. | 用平行单色光垂直照射不透明小圆板,在圆板后面屏上有圆板阴影中心处有一亮斑,这是光的干涉现象 | |
| D. | 用平行单色光垂直照射一把刀片,发现屏上刀片的阴影边缘模糊不清,这是光的衍射现象 |
7.在牛顿第二定律公式F=kma中,比例常数k的数值( )
| A. | 在任何情况下都等于1 | |
| B. | k值是由质量、加速度和力的大小决定的 | |
| C. | k值是由质量、加速度和力的单位决定的 | |
| D. | 在国际单位制中,k的数值一定等于1 |
14.关于α粒子的散射实验,下列说法正确的是( )
| A. | α粒子的散射实验现象有力地证明了汤姆生的原子结构模型 | |
| B. | 影响α粒子运动轨迹的主要因素是原子核 | |
| C. | 多数α粒子穿过金箔后沿直线前进,是因为它们离原子核较远 | |
| D. | 少数α粒子发生大角度的偏转,是因为它们穿过原子时,离核十分接近,受到很大的库伦斥力 |
 某同学在用如图所示的装置做“探究功与物体速度变化的关系”的实验中,先使小车不连接橡皮筋,在木板上恰能匀速下滑.再连接橡皮筋做实验.若第一、三次分别用一条、三条并在一起的相同橡皮筋做实验,且两次橡皮筋的伸长相同,则第三次实验中对小车做的功是第一次实验的3倍;由本实验可得出的结论是:功与速度的平方成正比.
某同学在用如图所示的装置做“探究功与物体速度变化的关系”的实验中,先使小车不连接橡皮筋,在木板上恰能匀速下滑.再连接橡皮筋做实验.若第一、三次分别用一条、三条并在一起的相同橡皮筋做实验,且两次橡皮筋的伸长相同,则第三次实验中对小车做的功是第一次实验的3倍;由本实验可得出的结论是:功与速度的平方成正比. 如图所示,等腰直角三角形OPQ,直角边OP、OQ长度均为L,直角平面内(包括边界)有一垂直平面向外的匀强磁场,磁感应强度大小为B.在PQ边下方放置一带电粒子发射装置,它沿垂直PQ边的方向发射出一束具有相同质量、电荷量和速度v的带正电粒子,已知带电粒子的比荷为:$\frac{q}{m}$=$\frac{2v}{BL}$.
如图所示,等腰直角三角形OPQ,直角边OP、OQ长度均为L,直角平面内(包括边界)有一垂直平面向外的匀强磁场,磁感应强度大小为B.在PQ边下方放置一带电粒子发射装置,它沿垂直PQ边的方向发射出一束具有相同质量、电荷量和速度v的带正电粒子,已知带电粒子的比荷为:$\frac{q}{m}$=$\frac{2v}{BL}$.