题目内容
质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力的作用.设某一时刻小球通过轨道最低点,此时绳子的张力为7mg,此后小球继续做运动,经过半个圆周恰能通过最高点,则在此过程中小球克服空气阻力做的功为:( )A.![]() mgR; B.
mgR; B.![]() mgR
mgR
C.![]() mgR; D.mgR.
mgR; D.mgR.
答案:C
解析:
提示:
解析:
| 如图所示,小球在最低点A时,由牛顿第二定律得:
7mg-mg=m 小球在最高点B时,由牛顿第二定律得: mg=m 小球从A经半个圆周运动到B的过程中由动能定理 W1+W2+…=ΔEK 得:W阻+WG=ΔEK 即:W阻-mg·2R= ∴ W阻=- 则:W克=|W阻|= |
提示:
| 小球从最低点到最高点通过这半个圆周的过程中,空气阻力大小未知,方向始终与速度方向相反,是变力.求此变力所做的功应从功和能的关系入手,由动能定理求出,但先应分别求出小球在最低点和最高点的动能. |

练习册系列答案
相关题目
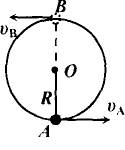
 质量为m的小球被系在轻绳一端,在竖直平面内做半径为R的圆周运动,如图所示,运动过程中小球受到空气阻力的作用.设某一时刻小球通过轨道的最低点,此时绳子的张力为7mg,在此后小球继续做圆周运动,经过半个圆周恰好能通过最高点,则在此过程中小球克服空气阻力所做的功是( )
质量为m的小球被系在轻绳一端,在竖直平面内做半径为R的圆周运动,如图所示,运动过程中小球受到空气阻力的作用.设某一时刻小球通过轨道的最低点,此时绳子的张力为7mg,在此后小球继续做圆周运动,经过半个圆周恰好能通过最高点,则在此过程中小球克服空气阻力所做的功是( ) 如图,质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受空气阻力的作用.某时刻小球通过轨道的最低点A,此时绳子的张力为7mg,此后小球继续做圆周运动,某时刻恰能通过最高点B,则在此过程中小球克服空气阻力所做的功为( )
如图,质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受空气阻力的作用.某时刻小球通过轨道的最低点A,此时绳子的张力为7mg,此后小球继续做圆周运动,某时刻恰能通过最高点B,则在此过程中小球克服空气阻力所做的功为( )