题目内容

4．一根不可伸缩的轻绳跨过轻质的定滑轮，一端挂一吊椅，另一端被坐在吊椅上的运动员拉住，如图所示．设运动员的质量为65kg，吊椅的质量为15kg，不计定滑轮与绳子间的摩擦，重力加速度取g=10m/s2．当运动员与吊椅一起正以加速度a=2m/s2上升时，试求：
（1）运动员竖直向下拉绳的力；
（2）运动员对吊椅的压力．

分析 （1）以人和吊椅为研究对象，对整体受力分析，由加速度，根据牛顿第二定律可以求得对绳的拉力；
（2）再对运动员为研究对象，根据牛顿第二定律求出支持力，从而结合牛顿第三定律求出压力的大小．

解答 解：（1）设运动员受到绳向上的拉力为F，由于跨过定滑轮的两段绳子拉力相等，吊椅受到绳的拉力也是F．对运动员和吊椅整体进行受力分析，则有：
2F-（m人+m椅）g=（m人+m椅）a
F=480N
由牛顿第三定律，运动员竖直向下拉绳的力
F'=480N
（2）设吊椅对运动员的支持力为FN，对运动员进行受力分析如图所示，则有：
F+FN-m人g=m人a
FN=300N
由牛顿第三定律，运动员对吊椅的压力也为300N．        
答：（1）运动员竖直向下拉绳的力为480N；
（2）运动员对吊椅的压力为300N．

点评 分析多个物体的受力时，一般先用整体法来求得共同的加速度，再用隔离法分析单个物体的受力，求得物体的受力情况，本题就是典型的应用整体隔离法的题目．

练习册系列答案
相关题目
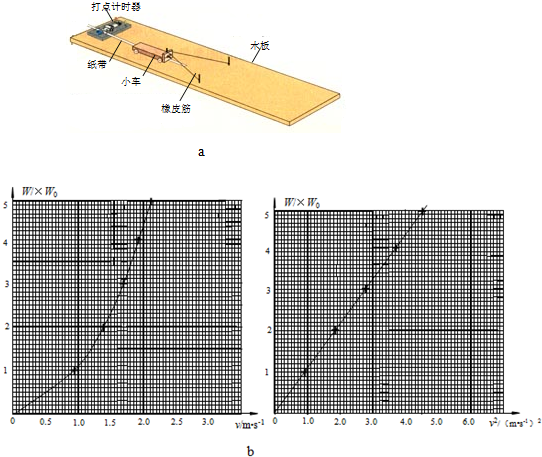
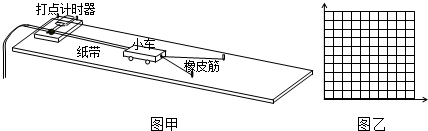
14．如图甲所示，是某研究性学习小组做探究“橡皮筋做的功和物体速度变化的关系”的实验，图中是小车在一条橡皮筋作用下弹出，沿木板滑行的情形，这时橡皮筋对小车做的功记为W． 当我们用2条、3条…完全相同的橡皮筋并在一起进行第2次、第3次…实验时，每次橡皮筋都拉伸到同一位置释放．小车每次实验中获得的速度由打点计时器所打的纸带测出．

（1）实验时为了使小车只在橡皮筋作用下运动，应采取的措施是；
（2）每次实验得到的纸带上的点并不都是均匀的，为了测量小车获得的速度，应选用纸带的部分进行测量；
（3）下面是本实验的数据记录表，请将第2次、第3次…实验中橡皮筋做的功填写在对应的位置；
次数/数据/物理量橡皮筋做的功Wn10个间隔的距离S、时间T小车速度vn小车速度平方vn2
1W0.200m0.2s1.01.0
22W0.280m0.2s1.41.96
33W0.300m0.2s1.52.25
44W0.400m0.2s2.04.0
55W0.450m0.2s2.25
（4）从理论上讲，橡皮筋做的功Wn和物体速度vn变化的关系应是Wn∝vn2． 请你运用数据表中测定的数据，在如图乙所示的坐标系中作出相应的图象验证理论的正确性；
（5）若在实验中你做出的图线与理论的推测不完全一致，你处理这种情况的做法是：分析误差来源或改进试验方案或测量手段，重新进行试验．
15．电子感应加速器（betatron）的基本原理如下：一个圆环真空室处于分布在圆柱形体积内的磁场中，磁场方向沿圆柱的轴线，圆柱的轴线过圆环的圆心并与环面垂直．圆中两个同心的实线圆代表圆环的边界，与实线圆同心的虚线圆为电子在加速过程中运行的轨道．已知磁场的磁感应强度B随时间t的变化规律为B=B0cos（$\frac{2πt}{T}$），其中T为磁场变化的周期．B0为大于0的常量．当B为正时，磁场的方向垂直于纸面指向纸外．若持续地将初速度为v0的电子沿虚线圆的切线方向注入到环内（如图），则电子在该磁场变化的一个周期内可能被加速的时间是（　　）
A．0～$\frac{T}{4}$B．$\frac{T}{4}$～$\frac{T}{2}$C．$\frac{T}{2}$～$\frac{3T}{4}$D．$\frac{3T}{4}$～T
12．为了“探究外力做功与物体动能变化的关系”，查资料得知，弹簧的弹性势能Ep=$\frac{1}{2}$kx2，其中k是弹簧的劲度系数，x是弹簧长度的变化量．
某同学就设想用压缩的弹簧推静止的小球（质量为m）运动来探究这一问题．
为了研究方便，把小铁球O放在水平桌面上做实验，让小球O在弹力作用下运动，即只有弹簧推力做功．
该同学设计实验如下：
首先进行如图甲所示的实验：将轻质弹簧竖直挂起来，在弹簧的另一端挂上小铁球O，静止时测得弹簧的伸长量为d．

在此步骤中，目的是要确定物理量弹簧劲度系数k，用m、d、g表示为$\frac{mg}{d}$．
接着进行如图乙所示的实验：将这根弹簧水平放在桌面上，一端固定，另一端被小铁球O压缩，测得压缩量为x，释放弹簧后，小铁球O被推出去，从高为h的水平桌面上抛出，小铁球O在空中运动的水平距离为L．
小铁球O的初动能Ek1=0．
小铁球O的末动能Ek2=$\frac{{mg{L^2}}}{4h}$．
弹簧对小铁球O做的功W=$\frac{{mg{x^2}}}{2d}$．（用m、x、d、g表示）
对比W和Ek2-Ek1就可以得出“外力做功与物体动能变化的关系”，即在实验误差允许范围内，外力所做的功等于物体动能的变化．
19．某实验小组的同学采用图所示的装置探究外力功与物体速度变化的关系．实验时，同学们先“平衡摩擦力”，即调节木板的倾角，使小车没有受到皮筋的拉力时正好匀速下滑．然后他们依次分别用1条，以及2条、3条、4条、5条同样的橡皮筋并在一起进行了5次实验．各次实验中，橡皮筋拉伸的长度都相同，小车在橡皮筋拉力的作用下，弹出并沿木板滑行，橡皮筋做功使小车获得的速度可通过打点计时器测出．图17b是利用数据软件进行数据处理后得到的W-v和W-v2图象．

（1）根据这两个图象可以得出的结论是：橡皮筋做的总功与小车获得的速度的平方成正比．（选填“速度”或“速度的平方”）
（2）如果实验小车的质量为0.20kg，则根据W-v2图象可知每一条橡皮筋对小车做的功W0为0.09J．
（3）实验中如果小车的速度过大，将导致纸带上打出的点迹过少，从而难以选择合适的点来计算小车的速度．解决这个问题可以采取的方法是：适当增加小车的质量
．
9．为了探究“合外力做功与物体动能改变的关系”，某同学设计了如下实验方案：
第一步：如图甲所示，把木板一端垫起，滑块通过跨过定滑轮的轻绳与一质量为m的重锤相连，重锤下连一纸带，纸带穿过打点计时器．调整木板倾角，直到轻推滑块，滑块沿木板向下匀速运动．
第二步：如图乙所示，保持木板倾角不变，取下细绳和重锤，将打点计时器安装在木板靠近定滑轮处，将滑块与纸带相连，使纸带穿过打点计时器，
第三步：接通电源释放滑块，使之从静止开始加速运动，打出的纸带如图丙所示．其中打下计数点0时，滑块的速度为零，相邻计数点的时间间隔为T．

（1）根据纸带求打点计时器打E点时滑块的速度vE=$\frac{{x}_{6}-{x}_{4}}{2T}$，
（2）合外力在OE段对滑块做功的表达式WOE=mgx5；（当地的重力加速度g）
（3）利用图丙数据求出各段合外力对滑块所做的功形及A、B、C、D、E各点的瞬间速度v，以v2为纵轴，以W为横轴建坐标系，作出v2-W图象，发现它是一条过坐标原点的倾斜直线，测得直线斜率为k，则滑块质量M=$\frac{2}{k}$．
16．在用自由落体法“探究动能定理”的实验中，

（1）为完成此实验，除了图1中所给的器材，以下所列器材中必需的有AD．（填字母）
A．毫米刻度尺       B．秒表     C．天平       D．低压交流6V电源
（2）图2为实验打下的纸带，纸带上的点都是连续打下的点．已知打点计时器所用交流电源周期为T，重力加速度为g．量得A、B、C各点到起点O（打下的第一个点）的长度分别是 h1、h2、h3．已知重锤质量为m，从起点O到B点重锤所受重力做功WG=mgh2，动能增加量△EK=$\frac{m（{h}_{3}-{h}_{1}）^{2}}{8{T}^{2}}$．（用题中所给字母表示）
（3）在实验中，WG和△EK增并不严格相等，产生误差的主要原因是重锤下落过程受到阻力作用．
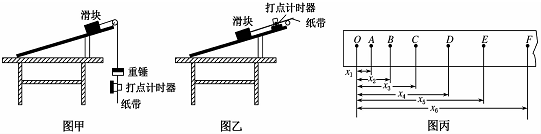
13．如图所示，物体沿斜面加速下滑，甲图中在物体上再放上一个小物体，乙图中在物体上加一个竖直向下的力F，下列关于物体运动的说法中正确的是（　　）
A．甲图中物体的加速度增大，乙图中物体的加速度增大
B．甲图中物体的加速度增大，乙图中物体的加速度不变
C．甲图中物体的加速度不变，乙图中物体的加速度增大
D．甲图中物体的加速度不变，乙图中物体的加速度不变
14．（1）如图1所示为某同学所安装的“验证牛顿第二定律”的实验装置．

①在“验证牛顿第二定律”的实验中，为了使小车受到合外力等于砝码和砝码盘的总重量，通常采用如下两个措施：
A．平衡摩擦力：将长木板无滑轮的一端下面垫一小木块，反复移动木块的位置，直到小车在砝码盘的拉动下带动纸带与小车一起做匀速直线运动；
B．在调整砝码多少的过程中，要保证砝码和砝码盘的总质量m远小于小车和砝码的总质量M．
以上哪一个措施中有何重大错误？（说明错误点）
②如图2是上述实验打出的一条纸带，已知打点计时器的打点周期是0.02s，结合图中给出的数据（单位cm），求出小车运动加速度的大小为4.0m/s2，并求出纸带中P点瞬时速度大小为2.6m/s（计算结果均保留2位有效数字）
（2）某实验小组设计了如图（a）所示的实验装置，通过改变重物的质量，利用计算机可得滑块运动的加速度a和所受拉力F的关系图象．他们在轨道水平和倾斜的两种情况下分别做了实验，得到了两条a-F图线，如图（b）所示．

①图线甲是在轨道左侧抬高成为斜面情况下得到的（选填“甲”或“乙”）；
②滑块和位移传感器发射部分的总质量m=0.5kg；滑块和轨道间的动摩擦因数μ=0.1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网