题目内容
质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图11所示.小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到O点(设两个小球直径相等,且远小于x0,略小于直圆筒内径).已知弹簧的弹性势能为![]() k·Δx2,其中k为弹簧的劲度系数,Δx为弹簧的形变量.求:
k·Δx2,其中k为弹簧的劲度系数,Δx为弹簧的形变量.求:
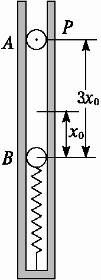
图11
(1)小球A的质量;
(2)小球A与小球B一起向下运动时速度的最大值.
(1)m′=m (2)vm=![]()
解析:
(1)由平衡条件可知:mg=kx0,设A的质量为m′,A由静止下落后与B接触前的瞬时速度为v1,
则m′g3x0=![]() m′v12,所以v1=
m′v12,所以v1=![]() 设A与B碰撞后的速度为v1′,有:m′v1=(m+m′)v1′,所以得到:
设A与B碰撞后的速度为v1′,有:m′v1=(m+m′)v1′,所以得到:![]() 由于A、B恰能回到O点,据动能定理有:
由于A、B恰能回到O点,据动能定理有:
-(m+m′)gx0+![]() kx02=0-
kx02=0-![]() (m+m′)v1′2,解得:m′=m.?
(m+m′)v1′2,解得:m′=m.?
(2)设由B点再向下运动x1时,它们的速度达到最大,此时它们的加速度为零,有:(m′+m)g=k(x1+x0),所以有x1=x0.据机械能守恒定律有:(m+m′)gx1+![]() (m+m′)v1′2+
(m+m′)v1′2+![]() kx02=
kx02=![]() (m+m′)vm2+
(m+m′)vm2+![]() k(x1+x0)2,解得:
k(x1+x0)2,解得:![]()

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
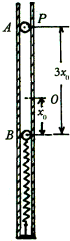 (2005?西城区模拟)质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于x0略小于直圆筒内径),已知弹簧的弹性势能为
(2005?西城区模拟)质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于x0略小于直圆筒内径),已知弹簧的弹性势能为
 质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为
质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为 ,其中k为弹簧的劲度系数,△x为弹簧的形变量.求:
,其中k为弹簧的劲度系数,△x为弹簧的形变量.求: