题目内容
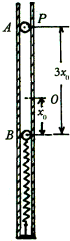 (2005?西城区模拟)质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于x0略小于直圆筒内径),已知弹簧的弹性势能为
(2005?西城区模拟)质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于x0略小于直圆筒内径),已知弹簧的弹性势能为| 1 | 2 |
(1)小球A质量.
(2)小球A与小球B一起向下运动时速度的最大值.
分析:(1)根据动能定理求出小球A与小球B相碰前的速度,再根据动量守恒定律求出碰后的速度,对A、B组成的系统,从B点到回到O点的过程,运用动能定理求出小球A的质量.
(2)当弹簧的弹力等于A、B两球的总重力时,小球A、B的速度最大,根据力的平衡求出两球下降的距离,再对系统运用机械能守恒定律,求出最大速度.
(2)当弹簧的弹力等于A、B两球的总重力时,小球A、B的速度最大,根据力的平衡求出两球下降的距离,再对系统运用机械能守恒定律,求出最大速度.
解答:解:(1)由平衡条件可知:mg=kx0
设A的质量为m',A由静止下落后与B接触前的瞬时速度为v1,则:m′g3x0=
m′
∴v1=
设A与B碰撞后的速度为v1',有:m'v1=(m+m')v1'∴v1′=
由于A、B恰能回到O点,据动能定理有:-(m+m′)gx0+
k
=0-
(m+m′)v1′2
解得:m'=m
(2)设由B点再向下运动x1时,它们的速度达到最大,此时它们的加速度为零,有:
据机械能守恒定律有:(m+m′)gx1+
(m+m′)v1′2+
k
=
(m+m′)vm2+
k(
+
)2
解得:vm=
答:(1)小球A质量等于m.
(2)小球A与小球B一起向下运动时速度的最大值为
.
设A的质量为m',A由静止下落后与B接触前的瞬时速度为v1,则:m′g3x0=
| 1 |
| 2 |
| v | 2 1 |
∴v1=
| 6gx0 |
设A与B碰撞后的速度为v1',有:m'v1=(m+m')v1'∴v1′=
| m′ |
| m+m′ |
| 6gx0 |
由于A、B恰能回到O点,据动能定理有:-(m+m′)gx0+
| 1 |
| 2 |
| x | 2 0 |
| 1 |
| 2 |
解得:m'=m
(2)设由B点再向下运动x1时,它们的速度达到最大,此时它们的加速度为零,有:
|
|
据机械能守恒定律有:(m+m′)gx1+
| 1 |
| 2 |
| 1 |
| 2 |
| x | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| x | 1 |
| x | 0 |
解得:vm=
| 2gx0 |
答:(1)小球A质量等于m.
(2)小球A与小球B一起向下运动时速度的最大值为
| 2gx0 |
点评:本题综合运用了动能定理、动量守恒定律、机械能守恒定律,综合性较强,关键是选择好研究的过程,运用合适的规律列表达式求解.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
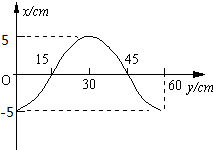 (2005?西城区模拟)如图所示为波源O振动1.5s时沿波的传播方向上部分质点振动的波形图,已知波源O在t=0时开始沿x轴负方向振动,t=1.5s时它正好第二次到达波谷,问:
(2005?西城区模拟)如图所示为波源O振动1.5s时沿波的传播方向上部分质点振动的波形图,已知波源O在t=0时开始沿x轴负方向振动,t=1.5s时它正好第二次到达波谷,问: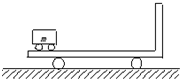 (2005?西城区模拟)如图所示,质量为M=20kg的平板车静止在光滑的水平面上;车上最左端停放着质量为m=5kg的电动车,电动车与平板车上的挡板相距L=5m.电动车由静止开始向右做匀加速运动,经时间t=2s电动车与挡板相碰,问:
(2005?西城区模拟)如图所示,质量为M=20kg的平板车静止在光滑的水平面上;车上最左端停放着质量为m=5kg的电动车,电动车与平板车上的挡板相距L=5m.电动车由静止开始向右做匀加速运动,经时间t=2s电动车与挡板相碰,问: