题目内容
4. 如图所示,在x轴上方有一竖直向下的匀强电场区域,电场强度大小为E=60V/m.x轴下方分布有多个磁感应强度大小为B=1T的条形匀强磁场区域,其宽度均为d1=3cm,相邻两磁场区域的间距为d2=4cm.现有一质量为m=6×10-13kg,电荷量为q=1×10-8C的带正电粒子(不计重力).
如图所示,在x轴上方有一竖直向下的匀强电场区域,电场强度大小为E=60V/m.x轴下方分布有多个磁感应强度大小为B=1T的条形匀强磁场区域,其宽度均为d1=3cm,相邻两磁场区域的间距为d2=4cm.现有一质量为m=6×10-13kg,电荷量为q=1×10-8C的带正电粒子(不计重力).(1)将带电粒子从y轴上坐标为y1处以平行于x轴的某一初速度射入电场区域,带电粒子运动经过x轴上坐标值为x1的Q点时,速度方向与x轴正方向的夹角为60°,且刚好不会穿出第一个匀强磁场区域,求y1和x1.
(2)若粒子从y轴上坐标为(0,50cm)的点处由静止释放,求自释放到粒子第二次过x轴的时间.
分析 (1)根据粒子刚好不会穿出第一个匀强磁场区域,画出运动轨迹,由几何关系找到圆周运动的半径,求出圆周运动的速度即为类平抛运动的末速度,根据运动的分解求出水平分速度和竖直分速度,由速度公式和位移公式即可求出y1和x1;
(2)粒子由静止释放,先在电场中做匀加速直线运动,进入磁场中做圆周运动,进入无磁场区域做匀速直线运动,画出粒子运动的轨迹,根据几何关系求出在磁场中运动的半径和圆心角,结合圆周运动的周期公式和匀变速直线运动的位移与时间公式,即可求出运动的总时间.
解答 解:(1)刚好不会穿出第一匀强磁场区域,画出运动的轨迹如图,
由几何关系:R(1-cos60°)=d1
解得:R=2d1=6cm,
带电粒子在匀强磁场中运动,洛伦兹力提供向心力:$qvB=m\frac{{v}^{2}}{R}$
解得:v=1×103m/s
带电粒子经过Q点时沿y轴方向的分速度:${v}_{y}=vsin60°=5\sqrt{3}×1{0}^{2}m/s$
由$a=\frac{Eq}{m}$
${v}_{y}^{2}=2a{y}_{1}$
联立解得:y1=0.375m=37.5cm
带电粒子经过Q点时沿x轴方向的分速度:${v}_{x}=vcos60°=5×1{0}^{2}m/s$
由${y}_{1}=\frac{1}{2}a{t}^{2}$解得$t=5\sqrt{3}×1{0}^{-4}$s
${x}_{1}={v}_{x}t=5×1{0}^{2}×5\sqrt{3}×1{0}^{-4}m=25\sqrt{3}cm$
(2)当带电粒子从y2=50cm的位置由静止释放后,先在电场中加速,加速时间t1满足${y}_{2}=\frac{1}{2}a{t}_{1}^{2}$,
解得:${t}_{1}=1×1{0}^{-3}s$
设粒子进入磁场时的速度大小为v2,在磁场中做圆周运动的轨道半径为R2,
由动能定理有:$qE{y}_{2}=\frac{1}{2}m{v}_{2}^{2}$
解得:v2=1×103m/s;

由$q{v}_{2}B=m\frac{{v}_{2}^{2}}{{R}_{2}}$,解得R2=6cm,
根据带电粒子在空间运动的轨迹可知,它最低能进入第二个磁场区域,
带电粒子经过第一个无磁场区域时运动方向与x轴的夹角θ满足:$cosθ=\frac{{d}_{1}}{{R}_{2}}=0.5$
解得:θ=60°
利用几何关系可知,带电粒子在磁场区域运动的总时间为半个圆周的运动时间:
${t}_{2}=\frac{1}{2}T=\frac{1}{2}•\frac{2π{R}_{2}}{{v}_{2}}=6π×1{0}^{-5}s$
带电粒子在无磁场区域的路程为:$s=\frac{2{d}_{2}}{sinθ}=\frac{4\sqrt{3}}{75}m$
运动时间:${t}_{3}=\frac{s}{{v}_{2}}=\frac{16\sqrt{3}}{3}×1{0}^{-5}s$
带电粒子自释放到第二次过x轴的时间:$t={t}_{1}+{t}_{2}+{t}_{3}=1.28×1{0}^{-3}$s
答:(1)y轴上坐标为y1=37.5cm,x轴上坐标值为${x}_{1}=25\sqrt{3}cm$.
(2)粒子自释放到第二次过x轴的时间为1.28×10-3s.
点评 本题考查带电粒子在电场、磁场中的运动及其相关的知识点,意在考查学生灵活运用运动的分解和合成、动能定理、牛顿运动定律及其相关知识解决问题的能力.运动过程较多,综合性较强,对作图能力要求较高,准确画出运动轨迹,并通过运动轨迹找几何关系,是解决这类问题的关键.

 综合自测系列答案
综合自测系列答案 如图所示的闭合电路中,R1、R2、R3是固定电阻,R4是半导体材料做出的光敏电阻,当开关S闭合后在没有光照射时,电容不带电,当用强光照射R4时,( )
如图所示的闭合电路中,R1、R2、R3是固定电阻,R4是半导体材料做出的光敏电阻,当开关S闭合后在没有光照射时,电容不带电,当用强光照射R4时,( )| A. | 电容C上板带正电 | B. | 电容C下板带正电 | ||
| C. | R4的阻值变大,路端电压增大 | D. | R4的阻值变小,电源总功率变小 |
 可以用如图所示的电路测量电源电动势和内电阻.R1、R2、R3是三个阻值均等于2Ω的电阻,当K接通时,伏特表的示数为1V,当K断开时,伏特表的示数为0.8V,则电源电动势和内电阻分别为( )
可以用如图所示的电路测量电源电动势和内电阻.R1、R2、R3是三个阻值均等于2Ω的电阻,当K接通时,伏特表的示数为1V,当K断开时,伏特表的示数为0.8V,则电源电动势和内电阻分别为( )| A. | ε=1.5V r=0.5Ω | B. | ε=2.0V r=1.0Ω | ||
| C. | ε=1.5V r=1.0Ω | D. | ε=2.0V r=0.5Ω |

(1)该小组将盐水柱作为纯电阻,粗测其电阻约为几千欧.现采用伏安法测盐水柱的电阻,有如下实验器材供选择:
A.直流电源:电动势12V,内阻很小,额定电流为1A;
B.电流表A1:量程0~10mA,内阻约10Ω;
C.电流表A2:量程0~600mA,内阻约0.5Ω;
D.电压表V:量程0~15V,内阻约15kΩ;
E.滑动变阻器R1:最大阻值10Ω;
F.滑动变阻器R2:最大阻值5kΩ;
G.开关、导线等
在可供选择的器材中,应选用的电流表是A1(填“A1”或“A2”),应该选用的滑动变阻器是R2(填“R1”或“R2”).
(2)该小组已经完成部分导线的连接,请你在如图1实物接线图中完成余下导线的连接.
(3)握住乳胶管的两端把它均匀拉长,多次实验测得盐水柱长度L、电阻R的数据如下表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 长度L(cm) | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 | 45.0 |
| 电阻R(kΩ) | 1.3 | 2.1 | 3.0 | 4.1 | 5.3 | 6.7 |
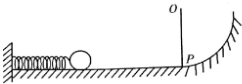 一个实验小组在“探究弹性势能的表达式”的实验中,利用了如图所示实验装置进行实验,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处,另有一小球,现在利用这些器材测定弹簧被压缩时的弹性势能.
一个实验小组在“探究弹性势能的表达式”的实验中,利用了如图所示实验装置进行实验,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处,另有一小球,现在利用这些器材测定弹簧被压缩时的弹性势能. 如图所示,一绝缘容器内部为立方体空腔,其长和宽分别为a和b,厚度为d,其两侧等高处装有两根与大气相通的玻璃管(可用来测量液体两侧的压强差).容器内装满密度为ρ的导电液体,容器上下两端装有铂电极A和C,这样就构成了一个液体电阻.该液体电阻置于一方向与容器的厚度方向平行的均匀恒定的磁感应强度为B的磁场中,并通过开关K接在一电动势为ε内阻为r的电池的两端.闭合开关.若稳定时两侧玻璃管中液面的高度差为h,求导电液体的电导率σ.重力加速度大小为g.
如图所示,一绝缘容器内部为立方体空腔,其长和宽分别为a和b,厚度为d,其两侧等高处装有两根与大气相通的玻璃管(可用来测量液体两侧的压强差).容器内装满密度为ρ的导电液体,容器上下两端装有铂电极A和C,这样就构成了一个液体电阻.该液体电阻置于一方向与容器的厚度方向平行的均匀恒定的磁感应强度为B的磁场中,并通过开关K接在一电动势为ε内阻为r的电池的两端.闭合开关.若稳定时两侧玻璃管中液面的高度差为h,求导电液体的电导率σ.重力加速度大小为g.