题目内容
8. 将一个小铁块(可看成质点)以一定的初速度沿倾角可在0-90°之间任意调整的木板向上滑动,设它沿木板向上能达到的最大位移为x,若木板倾角不同时对应的最大位移x与木板倾角α的关系如图所示,g=10m/s2.则( )
将一个小铁块(可看成质点)以一定的初速度沿倾角可在0-90°之间任意调整的木板向上滑动,设它沿木板向上能达到的最大位移为x,若木板倾角不同时对应的最大位移x与木板倾角α的关系如图所示,g=10m/s2.则( )| A. | 小铁块的初速度大小为v0=5m/s | |
| B. | 小铁块与木板间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$ | |
| C. | 当α=60°时,小铁块达到最高点后,又回到出发点,物体速度将变为5$\sqrt{2}$m/s | |
| D. | 当α=60°时,小铁块达到最高点后,又回到出发点,物体下滑的加速为$\frac{20}{3}$$\sqrt{3}$m/s2 |
分析 根据速度位移公式,结合牛顿第二定律,抓住α=90°和0°时对应的位移求出物体与斜面间的动摩擦因数和物体的初速度大小.由动能定理求出物体末速度,根据牛顿第二定律求出加速度的表达式,进而求出加速度.
解答 解:A、根据动能定理,物体沿斜面上滑过程有:
-mgsinα•x-μmgcosα•x=0-$\frac{1}{2}$m${{v}_{0}}^{2}$
解得:x=$\frac{{{v}_{0}}^{2}}{2g(sinα+μcosα)}$…①
由图可得,当α=90°时x=1.25m,根据v02=2gx,代入数据得:v0=5m/s,故A正确;
B、由图可得,α=30°时,x=1.25,①式代入数据得:μ=$\frac{\sqrt{3}}{3}$,故B正确;
C、把把α=60°代入①,解得:x=$\frac{5}{8}\sqrt{3}$m,由动能定理得:-μmgcosα•2x=$\frac{1}{2}m{{v}_{t}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$,代入数据得:${v}_{t}=\frac{5}{2}\sqrt{2}m/s$,故C错误;
D、下滑的加速度为:a=g(sinα-μcosα),当α=60°时,代入数据得:a=$\frac{\sqrt{3}}{3}$m/s2,故D错误;
故选:AB.
点评 本题考查了牛顿第二定律、运动学公式的综合,对于B答案,对数学要求能力较高,平时的学习中需加强训练.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
19.小船以一定的速度垂直河岸向对岸划行时,下列说法正确的是( )
| A. | 水流速度越大,小船运动的路程越长,时间不变 | |
| B. | 水流速度越大,小船运动的路程越长,时间越短 | |
| C. | 水流速度越大,小船运动的路程越长,时间越长 | |
| D. | 水流速度越大,小船运动的路程和时间都不变 |
16.一弹簧振子,当t=0时,物体处在x=-$\frac{A}{2}$(A为振幅)处且向负方向运动,则它的初相为( )
| A. | $\frac{π}{3}$ | B. | -$\frac{π}{3}$ | C. | -$\frac{2π}{3}$ | D. | $\frac{2π}{3}$ |
3.在“描绘小灯泡的伏安特性曲线”实验中,要测量一个标有“3V 1.5W”的灯泡两端的电压和通过它的电流,现有如下器材:

A.直流电源3V(内阻可不计) B.直流电流表0~600mA(内阻约0.5Ω) C.直流电压表0~3V(内阻约3kΩ) D.滑动变阻器(10Ω,1A)E.滑动变阻器(1kΩ,300mA) F.开关、导线若干
(1)本实验中滑动变阻器选用D(填“D”或“E”)
(2)某同学用导线a、b、c、d、e、f、g和h连接的电路如图1所示,电路中所有元器件都是完好的,且电压表和电流表已调零.闭合开关后发现电压表的示数为2V,电流表的示数为零,小灯泡不亮,则可确定断路的导线是d;若电压表示数为零,电流表的示数为0.3A,小灯泡亮,则断路的导线是h;若反复调节滑动变阻器,小灯泡亮度发生变化,但电压表、电流表示数不能调为零,则断路的导线是g.
(3)表中的各组数据是该同学在实验中测得的,根据表格中的数据在如图3所示的方格纸上作出该灯泡的伏安特性曲线.
(4)如图2所示,将两个这样的灯泡并联后再与5Ω的定值电阻R0串联,接在电压恒定为4V的电路上,每个灯泡的实际功率为0.30 w(结果保留两位有效数字).

A.直流电源3V(内阻可不计) B.直流电流表0~600mA(内阻约0.5Ω) C.直流电压表0~3V(内阻约3kΩ) D.滑动变阻器(10Ω,1A)E.滑动变阻器(1kΩ,300mA) F.开关、导线若干
(1)本实验中滑动变阻器选用D(填“D”或“E”)
(2)某同学用导线a、b、c、d、e、f、g和h连接的电路如图1所示,电路中所有元器件都是完好的,且电压表和电流表已调零.闭合开关后发现电压表的示数为2V,电流表的示数为零,小灯泡不亮,则可确定断路的导线是d;若电压表示数为零,电流表的示数为0.3A,小灯泡亮,则断路的导线是h;若反复调节滑动变阻器,小灯泡亮度发生变化,但电压表、电流表示数不能调为零,则断路的导线是g.
(3)表中的各组数据是该同学在实验中测得的,根据表格中的数据在如图3所示的方格纸上作出该灯泡的伏安特性曲线.
| U/V | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| I/A | 0 | 0.17 | 0.30 | 0.39 | 0.45 | 0.49 |
13.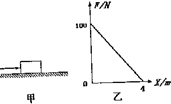 如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示,已知物体与底面间的动摩擦因数μ=0.5,g=10m/s2,下列说法正确的是( )
如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示,已知物体与底面间的动摩擦因数μ=0.5,g=10m/s2,下列说法正确的是( )
 如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示,已知物体与底面间的动摩擦因数μ=0.5,g=10m/s2,下列说法正确的是( )
如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示,已知物体与底面间的动摩擦因数μ=0.5,g=10m/s2,下列说法正确的是( )| A. | 物体先做加速运动,推力撤去时开始做减速运动 | |
| B. | 物体在水平面上运动的最大位移是10m | |
| C. | 物体运动的最大速度为2$\sqrt{15}$m/s | |
| D. | 物体在运动中的加速度先变小后不变 |
20.下列说法中正确的是( )
| A. | 布朗运动就是液中大量分子的无规则运动 | |
| B. | 布朗运动的剧烈程度与温度无关 | |
| C. | 固体很难被压缩,说明固体内分子之间只有相互的斥力 | |
| D. | 物体的温度越高,分子热运动越剧烈 |
17. 在光滑绝缘水平面的P点正上方O点固定了一电荷量为+Q的正点电荷,在水平面上的N点,由静止释放质量为m、电荷量为-q的带电小球,小球经过P点时速度为v,图中θ=60°,规定电场中P点的电势为零.则在+Q形成的电场中( )
在光滑绝缘水平面的P点正上方O点固定了一电荷量为+Q的正点电荷,在水平面上的N点,由静止释放质量为m、电荷量为-q的带电小球,小球经过P点时速度为v,图中θ=60°,规定电场中P点的电势为零.则在+Q形成的电场中( )
 在光滑绝缘水平面的P点正上方O点固定了一电荷量为+Q的正点电荷,在水平面上的N点,由静止释放质量为m、电荷量为-q的带电小球,小球经过P点时速度为v,图中θ=60°,规定电场中P点的电势为零.则在+Q形成的电场中( )
在光滑绝缘水平面的P点正上方O点固定了一电荷量为+Q的正点电荷,在水平面上的N点,由静止释放质量为m、电荷量为-q的带电小球,小球经过P点时速度为v,图中θ=60°,规定电场中P点的电势为零.则在+Q形成的电场中( )| A. | N点电势高于P点电势 | |
| B. | N点电势为-$\frac{m{v}^{2}}{2q}$ | |
| C. | P点电场强度大小是N点的2倍 | |
| D. | 带电小球在N点具有的电势能为-$\frac{1}{2}$mv2 |
18.下列叙述正确的有( )
| A. | 气体的压强越大,分子的平均动能越大 | |
| B. | 自然界中只要涉及热现象的实际过程都具有方向性 | |
| C. | 外界气体做正功,气体的内能一定增大 | |
| D. | 扩散现象与布朗运动都与温度有关 |
