��Ŀ����
12��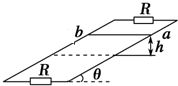 ��ͼ��ʾ�������㹻���Ĺ̶���ƽ�н�������λ����Ǧ�=30���б���ϣ������ϡ��¶˸�������ֵR=10���ĵ��裬��������������Բ��ƣ��������L=2m������������ƽ���ڶ��д�ֱ�ڵ���ƽ�����ϵ���ǿ�ų����Ÿ�Ӧǿ��B=0.5T������Ϊm=0.1kg������r=5���Ľ�����ab�ڽϸߴ��ɾ�ֹ�ͷţ�������ab���»�������ʼ���뵼�촹ֱ���뵼��Ӵ����ã���������ab�»��߶�h=3mʱ���ٶ�ǡ�ôﵽ���ֵv=2m/s����g=10m/s2������
��ͼ��ʾ�������㹻���Ĺ̶���ƽ�н�������λ����Ǧ�=30���б���ϣ������ϡ��¶˸�������ֵR=10���ĵ��裬��������������Բ��ƣ��������L=2m������������ƽ���ڶ��д�ֱ�ڵ���ƽ�����ϵ���ǿ�ų����Ÿ�Ӧǿ��B=0.5T������Ϊm=0.1kg������r=5���Ľ�����ab�ڽϸߴ��ɾ�ֹ�ͷţ�������ab���»�������ʼ���뵼�촹ֱ���뵼��Ӵ����ã���������ab�»��߶�h=3mʱ���ٶ�ǡ�ôﵽ���ֵv=2m/s����g=10m/s2��������1���������뵼��Ķ�Ħ��������
��2���������˶������е����¶˵���R�����繦�ʣ�
��3��������ab�������˶������в����Ľ����ȣ�
���� ��1��������ab�����»�ʱ�ٶȴﵽ����ɹ�ʽE=BLv�õ���Ӧ�綯�ƴ�С����ŷķ�������ab���еĸ�Ӧ����I���ɹ�ʽF=BIL������������ٸ���ƽ���������Ħ������С�����������Ħ��������
��2��������������ٶ��������Ӧ�綯�ƺ�Ӧ�������ɹ�ʽP=I2R������R�����繦�ʣ�
��3��������ab��е�ܵļ�����Ϊ��E=mgh-$\frac{1}{2}$mv2�����������غ㶨������������·�����ĵ��ȣ��ٸ��ݵ�·�����ӹ�ϵ���R�����Ľ����ȣ�
��� �⣺��1���ٶ����ʱ������ab�����ĵ綯��Ϊ��E=BLv=0.5��2��2V=2V
������·���ܵ���Ϊ��R��=$\frac{R}{2}$+r=10��
ab���еĸ�Ӧ����Ϊ��I=$\frac{E}{{R}_{��}}$=$\frac{2}{10}$A=0.2A
��ʱab�����ܵİ�����Ϊ��F=BIL=0.5��0.2��2N=0.2N
�������֪���ٶ����ʱ��ab���������˶������У�mgsin��=F+f
��ã�f=mgsin��-F=0.1��10��0.5-0.2=0.3N
�� f=��mgcos�ȵã���=$\frac{\sqrt{3}}{5}$
��3������R����������IR=$\frac{1}{2}I$=0.1A
����R�����繦��Ϊ��P=${I}_{R}^{2}$R=0.12��10W=0.1W
��3��������ab��е�ܵļ�����Ϊ��
��E=mgh-$\frac{1}{2}$mv2=0.1��10��3-0.5��0.1��22=2.8J
�������غ��������·�����ĵ���Ϊ��
Q=��E-f•$\frac{h}{sin30��}$=��2.8-0.3��3��2��J=1J
R�в�������Ϊ��QR=$\frac{1}{4}$Q=0.25��1J=0.25J
�𣺣�1���������뵼��Ķ�Ħ������Ϊ$\frac{\sqrt{3}}{5}$��
��2���������˶������е����¶˵���R�����繦��Ϊ0.1W��
��3��������ab�������˶������в����Ľ�������0.25W��
���� ���ǵ����ڵ����ϻ��������ͣ��������������Ƕ��о������ĽǶȣ��ؼ��ǰ������ķ����ͼ��㣮�ܵĽǶ�Ҫ�����������漰�����ܡ����������ת���ģ�

 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д� ��ͼ��ʾ����xOyƽ������ǿ�糡��һȺ���Ӵ�P����������Ե���ԲO����һ��λ�ã��Ƚ�Բ����Щλ�ã����ֵ���Բ��x��������Ľ���A��ʱ���������������������60eV����֪Բ�İ뾶��25cm����PAO=37�㣬����ǿ�糡�ĵ糡ǿ���ǣ�������
��ͼ��ʾ����xOyƽ������ǿ�糡��һȺ���Ӵ�P����������Ե���ԲO����һ��λ�ã��Ƚ�Բ����Щλ�ã����ֵ���Բ��x��������Ľ���A��ʱ���������������������60eV����֪Բ�İ뾶��25cm����PAO=37�㣬����ǿ�糡�ĵ糡ǿ���ǣ�������| A�� | 120V/m | B�� | 187.5V/m | C�� | 150V/m | D�� | 238.5V/m |
| A�� | ��������������������з������˶��Ķ��ܺͷ��ӵ����ܵ��ܺ� | |
| B�� | ������¶ȱ仯ʱ������ӵ�ƽ�����ܺͷ��ӵ�����Ҳ��֮�ı� | |
| C�� | ��������ȫ��ת��Ϊ����������Ҳ����ȫ��ת��Ϊ�� | |
| D�� | һ���������壬���������ʱ������ÿ��ƽ����ײ���ڵĴ��������¶ȵĽ��Ͷ���С | |
| E�� | ����ijһ���壬������û�й���ļ�����״����һ���й̶����۵� |
 ��ͼ��ʾ��С����a���ɾ�ֹ�������䣬��b��ʱ�뵯�ɽӴ�����c��ʱ���ɱ�ѹ������̣������Ƶ��������Ϳ�����������С����a��b��c���˶������У�������
��ͼ��ʾ��С����a���ɾ�ֹ�������䣬��b��ʱ�뵯�ɽӴ�����c��ʱ���ɱ�ѹ������̣������Ƶ��������Ϳ�����������С����a��b��c���˶������У�������| A�� | С��ļ��ٶ���ab�β��䣬��bc����С | |
| B�� | С����������ܼ��� | |
| C�� | С����b��ʱ�ٶ���� | |
| D�� | С��Ļ�е���غ� |
| A�� | ��$\frac{t-T}{t}$��${\;}^{\frac{2}{3}}$r | B�� | $\frac{t}{t-T}$r | C�� | ��$\frac{t}{t-T}$��${\;}^{\frac{2}{3}}$r | D�� | ��$\frac{t}{t+T}$��${\;}^{\frac{2}{3}}$r |

 ��̽�����������붯�ܸı�Ĺ�ϵʵ���У���֪ɰ��ɰͰ������Ϊm��С��������ΪM��Ϊ��ʵ���㣬��ʹС���ܵ��ĺ��������Կ���ɰ��ɰͰ�����������ش��������⣺
��̽�����������붯�ܸı�Ĺ�ϵʵ���У���֪ɰ��ɰͰ������Ϊm��С��������ΪM��Ϊ��ʵ���㣬��ʹС���ܵ��ĺ��������Կ���ɰ��ɰͰ�����������ش��������⣺ �ס��ҡ�������������ֱ�Ϊ2m��m��m�ųɵ�һֱ�߷��ڹ⻬ˮƽ���ϣ���ͼ��ʾ�������������һ����Ϊ��ֹ���������ٶ�v�������˶����������ڶ�����ײ����е����ʧ�����������յ��ٶȣ�
�ס��ҡ�������������ֱ�Ϊ2m��m��m�ųɵ�һֱ�߷��ڹ⻬ˮƽ���ϣ���ͼ��ʾ�������������һ����Ϊ��ֹ���������ٶ�v�������˶����������ڶ�����ײ����е����ʧ�����������յ��ٶȣ�