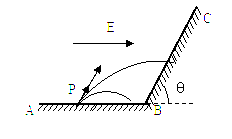题目内容
 如图:在一绝缘水平面上,一竖直绝缘挡板固定在O点,ON段表面粗糙,长度S=0.02m,NM段表面光滑,长度L=0.5m.在水平面的上方有一水平向左的匀强电场,场强为2×l05 N/C.有一小滑块质量为5×10-3kg,带正电,电量为 1×l0一7C,小滑块与ON段表面的动摩擦因数为0.4,将小滑块从M点由静止释放,小滑块在运动过程中没有电量损失,与挡板相碰时不计机械能损失.g取 l0m/S2.求:
如图:在一绝缘水平面上,一竖直绝缘挡板固定在O点,ON段表面粗糙,长度S=0.02m,NM段表面光滑,长度L=0.5m.在水平面的上方有一水平向左的匀强电场,场强为2×l05 N/C.有一小滑块质量为5×10-3kg,带正电,电量为 1×l0一7C,小滑块与ON段表面的动摩擦因数为0.4,将小滑块从M点由静止释放,小滑块在运动过程中没有电量损失,与挡板相碰时不计机械能损失.g取 l0m/S2.求:(1)小滑块从释放用多长时间第一次与挡板相碰?
(2)小滑块最后停在距离挡板多远的位置?
分析:(1)根据牛顿第二定律求得物体的加速度,然后使用运动学的公式分别求出物体在MN和NO上的时间,总时间即为所求;
(2)碰撞后的过程利用动能定理列方程即可求出距离;
(2)碰撞后的过程利用动能定理列方程即可求出距离;
解答:解:(1)在MN段电场力提供物体运动的加速度:a=
=
m/s2=4m/s2
由位移公式:L=
a
,
得:t1=
=
s=0.5s
物体达到N得时的速度:
v=at1=4×0.5m/s=2m/s
物体在NO段水平方向受到电场力和摩擦力的作用:qE-μmg=1×10-7×2×105N-0.4×5×10-3N=0
所以物体做匀速运动,t2=
=
s=0.01s
总时间:t=t1+t2=0.5+0.01=0.51s
(2)设经过n次碰撞后,停在距离挡板x处,由动能定理得:
qE(L+s-x)-μmg[(2n-1)s+x]=0
且:0<x≤s
解得:12.5<n<13.5,所以n取13,
代入上式解得:x=0.01m
答:(1)小滑块从释放用0.51s的时间第一次与挡板相碰;
(2)小滑块最后停在距离挡板0.01m远的位置.
| qE |
| m |
| 1×10-7×2×105 |
| 5×10-3 |
由位移公式:L=
| 1 |
| 2 |
| t | 2 1 |
得:t1=
|
|
物体达到N得时的速度:
v=at1=4×0.5m/s=2m/s
物体在NO段水平方向受到电场力和摩擦力的作用:qE-μmg=1×10-7×2×105N-0.4×5×10-3N=0
所以物体做匀速运动,t2=
| s |
| v |
| 0.02 |
| 2 |
总时间:t=t1+t2=0.5+0.01=0.51s
(2)设经过n次碰撞后,停在距离挡板x处,由动能定理得:
qE(L+s-x)-μmg[(2n-1)s+x]=0
且:0<x≤s
解得:12.5<n<13.5,所以n取13,
代入上式解得:x=0.01m
答:(1)小滑块从释放用0.51s的时间第一次与挡板相碰;
(2)小滑块最后停在距离挡板0.01m远的位置.
点评:本题要灵活的结合牛顿运动定律和动能定理等公式进行计算,难度中档.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
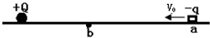 如图所示,绝缘水平面上固定一正点电荷Q,一质量为m、电荷量为-q的小滑块(可看作点电荷)从a点以初速度V0沿水平面向Q运动,到达b点时速度减为零.已知a、b间距离为s,滑块与水平面间的动摩擦因数为μ,重力加速度为g.以下判断正确的是( )
如图所示,绝缘水平面上固定一正点电荷Q,一质量为m、电荷量为-q的小滑块(可看作点电荷)从a点以初速度V0沿水平面向Q运动,到达b点时速度减为零.已知a、b间距离为s,滑块与水平面间的动摩擦因数为μ,重力加速度为g.以下判断正确的是( )A、此过程中产生的热能为
| ||||
B、滑块在运动过程的中间时刻,速度大小等于
| ||||
| C、滑块在运动过程中所受的库仑力一定小于滑动摩擦力 | ||||
D、Q产生的电场中,a、b两点间的电势差为Uab=
|
 (2008?普陀区一模)如图所示,在光滑绝缘水平面两端有两块平行带电金属板A、B,其间存在着场强E=200N/C的匀强电场,靠近正极板B处有一薄挡板S.一个带电小球,质量为m=1×10-2kg、电量q=-2×10-3C,开始时静止在P点,它与挡板S的距离为h=5cm,与A板距离为H=45cm.静止释放后小球在电场力的作用下向左运动,与挡板S相碰后电量减少到碰前的K倍,K=5/6,碰后小球的速度大小不变.
(2008?普陀区一模)如图所示,在光滑绝缘水平面两端有两块平行带电金属板A、B,其间存在着场强E=200N/C的匀强电场,靠近正极板B处有一薄挡板S.一个带电小球,质量为m=1×10-2kg、电量q=-2×10-3C,开始时静止在P点,它与挡板S的距离为h=5cm,与A板距离为H=45cm.静止释放后小球在电场力的作用下向左运动,与挡板S相碰后电量减少到碰前的K倍,K=5/6,碰后小球的速度大小不变.
 如图所示,在光滑绝缘水平面上方AB区间内存在水平向右的匀强电场,现有一根电荷分布均匀的绝缘细橡胶棒以v0=20m/s的初速度沿水平面从右侧进入电场区域,已知AB宽度D=1.0m,电场强度E=4×105N/C,绝缘细橡胶棒带电量q=+5×10-5C,质量m=0.01kg,长度L=0.072m,则细橡胶棒在电场内的过程中增加的电势能最大值为
如图所示,在光滑绝缘水平面上方AB区间内存在水平向右的匀强电场,现有一根电荷分布均匀的绝缘细橡胶棒以v0=20m/s的初速度沿水平面从右侧进入电场区域,已知AB宽度D=1.0m,电场强度E=4×105N/C,绝缘细橡胶棒带电量q=+5×10-5C,质量m=0.01kg,长度L=0.072m,则细橡胶棒在电场内的过程中增加的电势能最大值为