题目内容
如图所示,三个大小相同、质量均m的小球A、B、C静止在光滑水平面上,且A、B、C共线,现让A球以速度V0向B运动,A、B两球碰撞后粘在一起继续向右运动并与C球发生弹性碰撞,求最A、B、C的速度.

分析:A、B两球碰撞过程中动量守恒,根据动量守恒定律求出AB的共同速度,AB整体与C发生弹性碰撞,动量守恒,机械能守恒,根据动量守恒定律及机械能守恒定律列式即可求解.
解答:解:A、B两球碰撞过程中动量守恒,根据动量守恒定律得:
mv0=2mv1 ①
AB整体与C发生弹性碰撞,动量守恒,机械能守恒,根据动量守恒定律及机械能守恒定律得:
2mv1=2mvAB+mvC ②
×2mv12=
×2mvAB2+
×mvC2 ③
由①②③解得:
vAB=
,vC=
答:A、B的速度为
,C的速度为
.
mv0=2mv1 ①
AB整体与C发生弹性碰撞,动量守恒,机械能守恒,根据动量守恒定律及机械能守恒定律得:
2mv1=2mvAB+mvC ②
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由①②③解得:
vAB=
| v0 |
| 6 |
| 2v0 |
| 3 |
答:A、B的速度为
| v0 |
| 6 |
| 2v0 |
| 3 |
点评:本题主要考查了动量守恒定律及机械能守恒定律的应用,知道弹性碰撞过程中机械能守恒,难度适中.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
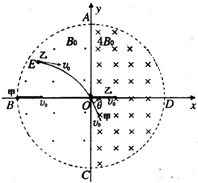
 如图所示,在以O为圆心,R为半径的圆形区域内,有一个水平方向的匀强磁场,磁感应强度大小为B,方向垂直于纸面向外,竖直平行放置的极板A、K相距为d,AK之间的电压可以调节,S1、S2为A、K极板上的两个小孔,且S1、S2和O三点在垂直极板的同一直线上,OS2=R,O点跟收集器D之间的距离为H,H>R,质量为m、电量为q的正离子经S1进入电场后,自S2向中心射去,不计离子进入电场时的初速度和重力,问:
如图所示,在以O为圆心,R为半径的圆形区域内,有一个水平方向的匀强磁场,磁感应强度大小为B,方向垂直于纸面向外,竖直平行放置的极板A、K相距为d,AK之间的电压可以调节,S1、S2为A、K极板上的两个小孔,且S1、S2和O三点在垂直极板的同一直线上,OS2=R,O点跟收集器D之间的距离为H,H>R,质量为m、电量为q的正离子经S1进入电场后,自S2向中心射去,不计离子进入电场时的初速度和重力,问: 如图所示,一个可看作质点的物体沿两个半径分别为R和r,相连接的半圆弧轨道从A点经B点运动到C点,A、B、C三点共线,则物体从A运动到C的位移大小和路程分别为( )
如图所示,一个可看作质点的物体沿两个半径分别为R和r,相连接的半圆弧轨道从A点经B点运动到C点,A、B、C三点共线,则物体从A运动到C的位移大小和路程分别为( )
 光滑绝缘水平面上有甲、乙、丙三个很小的金属球,质量均为m,甲不带电,乙带电量为+q,丙带电量为+
光滑绝缘水平面上有甲、乙、丙三个很小的金属球,质量均为m,甲不带电,乙带电量为+q,丙带电量为+
