题目内容
 如图所示,在以O为圆心,R为半径的圆形区域内,有一个水平方向的匀强磁场,磁感应强度大小为B,方向垂直于纸面向外,竖直平行放置的极板A、K相距为d,AK之间的电压可以调节,S1、S2为A、K极板上的两个小孔,且S1、S2和O三点在垂直极板的同一直线上,OS2=R,O点跟收集器D之间的距离为H,H>R,质量为m、电量为q的正离子经S1进入电场后,自S2向中心射去,不计离子进入电场时的初速度和重力,问:
如图所示,在以O为圆心,R为半径的圆形区域内,有一个水平方向的匀强磁场,磁感应强度大小为B,方向垂直于纸面向外,竖直平行放置的极板A、K相距为d,AK之间的电压可以调节,S1、S2为A、K极板上的两个小孔,且S1、S2和O三点在垂直极板的同一直线上,OS2=R,O点跟收集器D之间的距离为H,H>R,质量为m、电量为q的正离子经S1进入电场后,自S2向中心射去,不计离子进入电场时的初速度和重力,问:(1)为使正离子经S2进入磁场做圆周运动后,以跟进入时的速度相垂直的方向离开磁场,A、K之间的电压应为多大?
(2)在满足(1)的条件下,离子自S1到收集器D总共需要多少时间?
分析:(1)根据粒子在磁场中运动的轨道半径等于R,结合洛伦兹力提供向心力求出速度的大小,从而根据动能定理求出A、K间的电压 大小.
(2)粒子在电场中做匀加速直线运动,在磁场中做匀速圆周运动,出磁场后做匀速直线运动,结合运动学公式求出三段时间,从而得出离子自S1到收集器D总共需要的时间.
(2)粒子在电场中做匀加速直线运动,在磁场中做匀速圆周运动,出磁场后做匀速直线运动,结合运动学公式求出三段时间,从而得出离子自S1到收集器D总共需要的时间.
解答:解:(1)正离子在电场中做初速度为零的匀加速直线运动,
由动能定理得qU=
mv2①
∵正离子以速度v进入匀强磁场,做匀速圆周运动Bqv=m
②
正离子离开了磁场时的速度与进入时相垂直,故r=R ③
解得A、K间的电压U=
(2)正离子在电场中的运动时间t1=
=
=
在磁场中的运动时间t2=
T=
?
=
在磁场与收集器之间运动时间t3=
=
离子自S1到收集器D的总时间t=
(
+
)
答:(1)A、K之间的电压应为U=
.
(2)在满足(1)的条件下,离子自S1到收集器D总共需要t=
(
+
).
由动能定理得qU=
| 1 |
| 2 |
∵正离子以速度v进入匀强磁场,做匀速圆周运动Bqv=m
| v2 |
| r |
正离子离开了磁场时的速度与进入时相垂直,故r=R ③
解得A、K间的电压U=
| B2R2q |
| 2m |
(2)正离子在电场中的运动时间t1=
| v |
| a |
| mvd |
| qU |
| 2md |
| BqR |
在磁场中的运动时间t2=
| 1 |
| 4 |
| 1 |
| 4 |
| 2πm |
| Bq |
| πm |
| 2Bq |
在磁场与收集器之间运动时间t3=
| H-R |
| v |
| (H-R)m |
| BqR |
离子自S1到收集器D的总时间t=
| m |
| Bq |
| 2d+H-R |
| R |
| π |
| 2 |
答:(1)A、K之间的电压应为U=
| B2R2q |
| 2m |
(2)在满足(1)的条件下,离子自S1到收集器D总共需要t=
| m |
| Bq |
| 2d+H-R |
| R |
| π |
| 2 |
点评:本题考查了带电粒子在电场、磁场中的运动,知道粒子的运动规律,结合牛顿第二定律和运动学公式进行分析求解.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
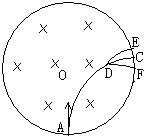 (2004?惠州一模)如图所示,在一个半径为R的圆形区域内存在着匀强磁场,磁场方向垂直于圆面向里,一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内,粒子将做圆周运动到达磁场边界的C点,但在粒子经过D点时,恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子,关于这个新粒子的运动情况,以下判断正确的是( )
(2004?惠州一模)如图所示,在一个半径为R的圆形区域内存在着匀强磁场,磁场方向垂直于圆面向里,一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内,粒子将做圆周运动到达磁场边界的C点,但在粒子经过D点时,恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子,关于这个新粒子的运动情况,以下判断正确的是( ) 如图所示,在圆心O处固定一正点电荷,现从P点以相同的速率发射两个检验电荷a、b,分别沿PM、PN运动到M、N两点,M、N都在以O为圆心的圆上.若检验电荷a、b的质量、电荷量均相等,则下列判断正确的是( )
如图所示,在圆心O处固定一正点电荷,现从P点以相同的速率发射两个检验电荷a、b,分别沿PM、PN运动到M、N两点,M、N都在以O为圆心的圆上.若检验电荷a、b的质量、电荷量均相等,则下列判断正确的是( ) 如图所示,在圆心O处固定一正点电荷,两个质量和电量均相同的检验电荷a、b从P点以相同的速率,分别沿PN、PM运动到N、M(均在以O为圆心的圆上),下列说法正确的是( )
如图所示,在圆心O处固定一正点电荷,两个质量和电量均相同的检验电荷a、b从P点以相同的速率,分别沿PN、PM运动到N、M(均在以O为圆心的圆上),下列说法正确的是( )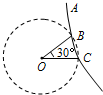 如图所示,在点O置于一个正点电荷,在过点O的竖直平面内的点A处,自由释放一个带正电的小球,小球的质量为m,带电量为q,小球落下的轨迹如图中实线所示,它与以O为圆心,R为半径的圆相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC高度为h,若小球过B点时的速度为v,则( )
如图所示,在点O置于一个正点电荷,在过点O的竖直平面内的点A处,自由释放一个带正电的小球,小球的质量为m,带电量为q,小球落下的轨迹如图中实线所示,它与以O为圆心,R为半径的圆相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC高度为h,若小球过B点时的速度为v,则( )