题目内容
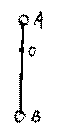
如图所示,轻杆长3L,杆两端分别固定质量为m的A球和质量为3m的B球,杆上距A球为L处的O点安装在水平转轴上,杆在转轴的带动下在竖直面内转动,试问:(1)若A球运动到最高点时,杆OA对球A没有力作用,此时水平轴的力多大?
(2)当杆转动的角速度为多少时,杆处于竖直位置时水平轴刚好不受力作用?

【答案】分析:(1)若A球运动到最高点时,杆OA对球A没有力作用,对A,重力提供向心力,对B,合力提供向心力,根据向心力公式列式即可求解;
(2)杆对两球的作用力大小相等、方向相反,轴才不变力.根据分析可知,此时A球应在下方,B球应在上方,分别对AB根据向心力公式列式即可求解;
解答:解:(1)设杆对B球的拉力为T,则有
解得:T=9mg
所以杆对轴的作用为T'=9mg.
(2)杆对两球的作用力大小相等、方向相反,轴才不受力.根据分析可知,
此时A球应在下方,B球应在上方,由此得,
对B球:3mg+T=3mω?2L
对A球:T-mg=m?ω2?L
解得:
答:(1)若A球运动到最高点时,杆OA对球A没有力作用,此时水平轴的力为9mg;
(2)当杆转动的角速度为 时,杆处于竖直位置时水平轴刚好不受力作用.
时,杆处于竖直位置时水平轴刚好不受力作用.
点评:本题关键要对两球分别受力分析,找出其向心力来源,根据牛顿第二定律列式求解;
(2)杆对两球的作用力大小相等、方向相反,轴才不变力.根据分析可知,此时A球应在下方,B球应在上方,分别对AB根据向心力公式列式即可求解;
解答:解:(1)设杆对B球的拉力为T,则有

解得:T=9mg
所以杆对轴的作用为T'=9mg.
(2)杆对两球的作用力大小相等、方向相反,轴才不受力.根据分析可知,
此时A球应在下方,B球应在上方,由此得,
对B球:3mg+T=3mω?2L
对A球:T-mg=m?ω2?L
解得:

答:(1)若A球运动到最高点时,杆OA对球A没有力作用,此时水平轴的力为9mg;
(2)当杆转动的角速度为
 时,杆处于竖直位置时水平轴刚好不受力作用.
时,杆处于竖直位置时水平轴刚好不受力作用.点评:本题关键要对两球分别受力分析,找出其向心力来源,根据牛顿第二定律列式求解;

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
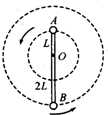 如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,已知球B运动到最高点时,球B对杆恰好无作用力.求:
如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,已知球B运动到最高点时,球B对杆恰好无作用力.求: 如图所示,轻杆长3L,杆两端分别固定质量为m的A球和质量为3m的B球,杆上距A球为L处的O点安装在水平转轴上,杆在转轴的带动下在竖直面内转动,试问:
如图所示,轻杆长3L,杆两端分别固定质量为m的A球和质量为3m的B球,杆上距A球为L处的O点安装在水平转轴上,杆在转轴的带动下在竖直面内转动,试问: 如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,已知球B运动到最高点时,球B对杆恰好无作用力.求:
如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,已知球B运动到最高点时,球B对杆恰好无作用力.求: