题目内容

如图所示，电荷量均为＋q、质量分别为m和2m的小球A和B．中间连接质量不计的细绳，重力加速度为g，在竖直方向的匀强电场中以速度v0匀速下落，某时刻细绳断开(不考虑电荷间的库仑力作用)，求：

(1)细绳断开后，A，B两球的加速度的大小和方向

(2)自绳断开至A球速度为零的过程中，B球电势能增量

答案：
解析：

　　解：(1)设电场强度为E，把小球A、B看作一个系统，由于绳未断前作匀速运动，则有

　　2qE＝3mg，E＝3mg/2q　(1分)

　　绳断后，根据牛顿第二定律：

　　对A：qE－mg＝maA

　　得aA＝g/2，方向竖直向上　(2分)

　　对B：qE－2mg＝2maB

　　得aB＝－g/4，负号表示方向竖直向下　(2分)

　　(2)细绳断开前后两球组成系统合外力为零，满足总动量守恒，设A球速度为零时，B球的速度为vB，根据动量守恒定律得：

　　(m＋2m)v0＝2mvB＋0　(2分)

　　VB＝1.5v0　(1分)

　　对B球有：由动能定理得F合SB＝　(2分)

　　

　　ΔEA＝qEsB＝3.75m v02　(1分)


练习册系列答案
相关题目
如图所示，电荷量均为+q、质量分别为m和2m的小球A和B．中间连接质量不计的细绳，在竖直方向的匀强电场中以速度v0匀速上升，某时刻细绳断开（不考虑电荷间的库仑力作用），求：
（1）细绳断开后，A，B两球的加速度的大小和方向．
（2）当B球速度为零时，A球的速度大小．
（3）自绳断开至B球速度为零的过程中，A球机械能增量．
（2005?杭州一模）如图所示，电荷量均为+q，质量分别为m和2m的小球A和B，中间连接质量不计的细绳，在竖直方向的匀强电场中以速度v0匀速上升，某时刻细绳突然断开．不计两球间的库仑力，求：
（1）电场的场强E及细绳断开后A、B两球的加速度；
（2）当B球速度为零时，A球速度的大小；
（3）自细绳断开至B球速度变为零的过程中，两球组成的系统的机械能增加量．
如图所示，电荷量均为+q、质量分别为m和3m的小球A和B，中间连接质量不计的细绳，在竖直方向的匀强电场中以速度v0匀速上升．若不计两带电小球间的库仑力作用，某时刻细绳断开，求：
（1）电场强度及细绳断开后A、B两球的加速度；
（2）当B球速度为零时，A球速度的大小；
（3）从绳断开至B球速度为零的过程中，两球组成系统的机械能增量为多少？
如图所示，电荷量均为+Q的点电荷A、B连线上有a、c两点，在连线的中垂线上有b、d两点，a、b、c、d点都与连线的中点O等距．下列说法中正确的是（　　）
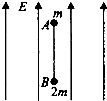精英家教网如图所示，电荷量均为+q、质量分别为m和2m的小球A和B，中间连接质量不计的绝缘细绳（不考虑电荷之间的库仑力），在竖直方向的匀强电场中以速度v0匀速上升，某时刻细绳断开．求：
（1）电场强度大小及细绳断开后两球A、B的加速度；
（2）当球B速度为零时，球A的速度大小．
（3）自绳断开至球B速度为零的过程中，两球组成系统的机械能增量为多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网