题目内容
18. 如图所示,一半圆形区域内存在垂直于纸面向外的匀强磁场,O为圆心,AD为直径,C为半圆弧的中点,B为AC弧的中点,现将两个比荷相同带正电粒子分别从A、B两点沿垂直于OC的方向射入磁场中,结果两粒子均从C点离开磁场,设两粒子在磁场中运动的时间分别为t1、t2,它们射入磁场的速度大小分别为v1、v2,则下列判断正确的是( )
如图所示,一半圆形区域内存在垂直于纸面向外的匀强磁场,O为圆心,AD为直径,C为半圆弧的中点,B为AC弧的中点,现将两个比荷相同带正电粒子分别从A、B两点沿垂直于OC的方向射入磁场中,结果两粒子均从C点离开磁场,设两粒子在磁场中运动的时间分别为t1、t2,它们射入磁场的速度大小分别为v1、v2,则下列判断正确的是( )| A. | t1=t2 | B. | t1<t2 | C. | v1>v2 | D. | v1=v2 |
分析 根据粒子的入射点与出射点的位置,画出粒子运动的轨迹,然后结合几何关系得出粒子运动的半径与磁场区域的半径之间的关系,再根据半径公式即可比较速度关系;个偏转的角度与周期的关系即可求出运动的时间.
解答 解:如图,分别画出它们运动的轨迹,设AO=R
由几何关系可知,RA=R;
${R}_{B}^{2}=[{{R}_{B}-(1-\frac{\sqrt{2}}{2})R)}^{2}+(\frac{\sqrt{2}}{2}R)^{2}$
整理得:RB=R
A、B、粒子在磁场中运动,洛伦兹力提供向心力,得:$qvB=\frac{m{v}^{2}}{r}$,所以:$r=\frac{mv}{qB}$
粒子运动的周期:T=$\frac{2πr}{v}=\frac{2πm}{qB}$粒子的比荷相等,则周期相等,与运动的速度无关,由图可知,从A点射入的粒子的偏转角度大,根据:
$\frac{t}{T}=\frac{θ}{2π}$,可知t1>t2.故A错误,B错误;
C、D、由以上的分析可知,两种情况下粒子运动的半径是相等的,根据半径公式$r=\frac{mv}{qB}$可知,粒子的速度是相等的.故C错误,D正确.
故选:D
点评 该题考查带电粒子在磁场中的运动,两种情况下,粒子的入射点虽然不同,只要画出运动的根据,并结合图中的几何关系确定两种情况下的半径相等,即可正确解答.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
6.物体1的重力势能Ep1=3J,物体2的重力势能Ep2=-3J,则( )
| A. | Ep1=Ep2 | B. | Ep1>Ep2 | C. | Ep1<Ep2 | D. | 无法判断 |
9. 如图所示,面积为0.02m2、内阻不计的100匝矩形线圈ABCD,绕垂直于磁场的轴OO′匀速转动,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T.矩形线圈通过滑环与理想变压器相连,触头P可移动,副线圈所接电阻R=50Ω,电表均为理想交流电表.当线圈平面与磁场方向平行时开始计时.下列说法正确的是( )
如图所示,面积为0.02m2、内阻不计的100匝矩形线圈ABCD,绕垂直于磁场的轴OO′匀速转动,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T.矩形线圈通过滑环与理想变压器相连,触头P可移动,副线圈所接电阻R=50Ω,电表均为理想交流电表.当线圈平面与磁场方向平行时开始计时.下列说法正确的是( )
 如图所示,面积为0.02m2、内阻不计的100匝矩形线圈ABCD,绕垂直于磁场的轴OO′匀速转动,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T.矩形线圈通过滑环与理想变压器相连,触头P可移动,副线圈所接电阻R=50Ω,电表均为理想交流电表.当线圈平面与磁场方向平行时开始计时.下列说法正确的是( )
如图所示,面积为0.02m2、内阻不计的100匝矩形线圈ABCD,绕垂直于磁场的轴OO′匀速转动,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T.矩形线圈通过滑环与理想变压器相连,触头P可移动,副线圈所接电阻R=50Ω,电表均为理想交流电表.当线圈平面与磁场方向平行时开始计时.下列说法正确的是( )| A. | 线圈中感应电动势的表达式为e=100cos(100t)V | |
| B. | P上移时,电流表示数减小 | |
| C. | t=0时,电压表示数为100$\sqrt{2}$V | |
| D. | 当原、副线圈匝数比为2:1时,电阻上消耗的功率为50W |
6.下列说法正确的是( )
| A. | 速度的变化量越大,加速度就越大 | |
| B. | 在匀变速直线运动中,速度方向与加速度方向一定相同 | |
| C. | 平抛运动是匀变速曲线运动 | |
| D. | 匀速圆周运动的线速度、角速度、周期都不变 |
10.有一星球的质量为地球质量的32倍,它表面附近的重力加速度是地球表面附近重力加速度的2倍,则该星球的密度约是地球密度的( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2倍 | D. | 8倍 |
8.在物理学发展的过程中,某位科学家开创了以实验检验猜想和假设的科学方法,并用这种方法研究了落体运动的规律,这位科学家是( )
| A. | 焦耳 | B. | 库仑 | C. | 伽利略 | D. | 法拉第 |
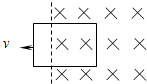 如图所示,先后以速度v1和v2(v1=2v2),匀速地把同一线圈从同一位置拉出有界匀强磁场的过程中,在先后两种情况下,
如图所示,先后以速度v1和v2(v1=2v2),匀速地把同一线圈从同一位置拉出有界匀强磁场的过程中,在先后两种情况下, 如图为一水平传送带装置的示意图.传送带的左端与光滑曲面轨道平滑连接,右端与光滑圆轨道相切,MN是圆轨道的一条竖直直径,将一质量m=1kg的小物块乙轻轻放在传送带上距B点2m处的P点,质量也为m=1kg小物块甲置于距B点高度为h1=5m的光滑曲面上的A点,当传送带静止时,让甲由静止下滑与静止在传送带上小物块乙发生弹性正碰,碰撞过程无能量损失,碰撞后乙恰好能到达光滑圆轨道上的最高点N,已知圆轨道半径r=0.4m,两小物块与传送带间的动摩擦因数为μ=0.5,重力加速度g=10m/s2.求:
如图为一水平传送带装置的示意图.传送带的左端与光滑曲面轨道平滑连接,右端与光滑圆轨道相切,MN是圆轨道的一条竖直直径,将一质量m=1kg的小物块乙轻轻放在传送带上距B点2m处的P点,质量也为m=1kg小物块甲置于距B点高度为h1=5m的光滑曲面上的A点,当传送带静止时,让甲由静止下滑与静止在传送带上小物块乙发生弹性正碰,碰撞过程无能量损失,碰撞后乙恰好能到达光滑圆轨道上的最高点N,已知圆轨道半径r=0.4m,两小物块与传送带间的动摩擦因数为μ=0.5,重力加速度g=10m/s2.求: 如图甲为某探究小组为测定动摩擦因数的设置,水平平台的右端安装有轻质定滑轮,质量为M=2.5kg的物块A放在与滑轮相距L的平台上,现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m=0.5kg的小球B,绳拉直时用手托住小球使其在距地面高h处静止,绳与滑轮间的摩擦不计,重力加速度为g(g取10m/s2).设最大静摩擦力等于滑动摩擦力.由静止释放小球,系统运动,该小组对小球匀加速下落过程拍得同一底片上多次曝光的照片如图(乙)所示,拍摄时每隔1秒曝光一次,若小球直径为20cm,则系统加速度等于0.4m/s2,物块A与平台间的动摩擦因数μ=0.152.
如图甲为某探究小组为测定动摩擦因数的设置,水平平台的右端安装有轻质定滑轮,质量为M=2.5kg的物块A放在与滑轮相距L的平台上,现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m=0.5kg的小球B,绳拉直时用手托住小球使其在距地面高h处静止,绳与滑轮间的摩擦不计,重力加速度为g(g取10m/s2).设最大静摩擦力等于滑动摩擦力.由静止释放小球,系统运动,该小组对小球匀加速下落过程拍得同一底片上多次曝光的照片如图(乙)所示,拍摄时每隔1秒曝光一次,若小球直径为20cm,则系统加速度等于0.4m/s2,物块A与平台间的动摩擦因数μ=0.152.