题目内容
1.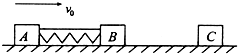 如图所示,光滑水平直轨道上有三个滑块A、B、C,质量分别为mA=m,mB=mC=2m,A、B用细绳连接,中间有一压缩的轻弹簧(弹簧与滑块不栓接).开始时A、B以共同速度v0运动,C静止.某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同.求:
如图所示,光滑水平直轨道上有三个滑块A、B、C,质量分别为mA=m,mB=mC=2m,A、B用细绳连接,中间有一压缩的轻弹簧(弹簧与滑块不栓接).开始时A、B以共同速度v0运动,C静止.某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同.求:(1)B与C碰撞前B的速度
(2)B与C碰撞前后,机械能的损失为多少?
分析 (1)A、B组成的系统,在细绳断开的过程中动量守恒,B与C碰撞过程中动量守恒,抓住三者最后速度相同,根据动量守恒定律求出B与C碰撞前B的速度.
(2)根据能量守恒定律可以求出损失的机械能.
解答 解:(1)A、B被弹开过程A、B系统动量守恒,以向右为正方向,
由动量守恒定律得:(mA+mB)v0=mAvA+mBvB,
对整个过程,由动量守恒定律得:(mA+mB)v0=(mA+mB+mC)vB,
解得:vA=$\frac{3}{5}$v0,vB=$\frac{6}{5}$v0;
(2)由能量守恒定律可知,B、C碰撞前后损失的机械能:
△E=$\frac{1}{2}$mBvB2-$\frac{1}{2}$(mB+mC)vA2,解得:△E=$\frac{18}{25}$mv02;
答:(1)B与C碰撞前B的速度为$\frac{6}{5}$v0.
(2)B与C碰撞前后,机械能的损失为为$\frac{18}{25}$mv02.
点评 本题综合考查了动量守恒定律和能量守恒定律,综合性较强,对学生的能力要求较高,要加强这方面的训练.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
11.三个一定质量的带电小球放在光滑绝缘水平面上,其中A、B小球固定,C小球在AB正中间处恰保持静止,则( )
| A. | 若A球带正电、C球带负电,将A球沿AB连线缓慢远离B球,则C球也将缓慢离开B球 | |
| B. | 若A球带正电、C球带正电,将A球沿AB连线缓慢靠近B球,则C球也将缓慢靠近B球 | |
| C. | 若三球带同种电荷,将A球带电量突然减小为某一值,C球将一直做加速度越来越小的运动 | |
| D. | 若三球带同种电荷,将C球从平衡位置略微向正上方拉起后静止释放,C球不可能静止 |
16.下列说法正确的是( )
| A. | 布朗运动反映了液体分子的无规则运动 | |
| B. | 给自行车轮胎打气,越来越费力,说明气体分子间斥力在增大 | |
| C. | 放在水面上的硬币可以浮在水面上是因为硬币所受浮力等于重力 | |
| D. | 利用太阳能装置使机械长久运动下去,这并不违背热力学第二定律 |
6. 竖直向上的匀强磁场中,水平放置一单匝金属圆形线圈,线圈所围的面积为0.1m2,线圈的电阻为1Ω.规定图(a)所示感应电流的方向为正方向.磁场的磁感应强度B随时间t的变化规律如图(b)所示,则以下说法正确的是( )
竖直向上的匀强磁场中,水平放置一单匝金属圆形线圈,线圈所围的面积为0.1m2,线圈的电阻为1Ω.规定图(a)所示感应电流的方向为正方向.磁场的磁感应强度B随时间t的变化规律如图(b)所示,则以下说法正确的是( )
 竖直向上的匀强磁场中,水平放置一单匝金属圆形线圈,线圈所围的面积为0.1m2,线圈的电阻为1Ω.规定图(a)所示感应电流的方向为正方向.磁场的磁感应强度B随时间t的变化规律如图(b)所示,则以下说法正确的是( )
竖直向上的匀强磁场中,水平放置一单匝金属圆形线圈,线圈所围的面积为0.1m2,线圈的电阻为1Ω.规定图(a)所示感应电流的方向为正方向.磁场的磁感应强度B随时间t的变化规律如图(b)所示,则以下说法正确的是( )| A. | 第1s内,线圈具有扩张趋势 | |
| B. | 第3s内,线圈的发热功率最大 | |
| C. | 第4s时,感应电流的方向为负 | |
| D. | 0~5 s时间内,感应电流的最大值为0.1A |
10.当航天飞机在环绕地球的轨道上飞行时,从中释放一颗卫星,卫星与航天飞机保持相对静止,两者用导线电缆相连,这种卫星称为绳系卫星.现有一颗绳系卫星在地球赤道上空自西向东运行.卫星位于航天飞机正上方,它与航天飞机间的距离是20.5km(远小于航天飞机的轨道半径),卫星所在位置的地磁场为B=4.6×10-5,磁场沿水平方向由南向北.航天飞机和卫星的运行速度为7.6km/s,则( )
| A. | 缆绳中的感应电动势的大小为3.6×103V | |
| B. | 缆绳中的感应电动势的大小为7.2×103V | |
| C. | 缆绳靠近绳系卫星一端的电势高 | |
| D. | 缆绳靠近航天飞机一端的电势高 |
 如图所示,质量mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B以初速度v0=10m/s沿水平方向向右运动,与A碰撞后都向右运动.木块A与挡板碰撞后立即反弹(设木块A与挡板碰撞过程无机械能损失).后来木块A与B发生二次碰撞,碰后A、B同向运动,速度大小分别为1m/s、4m/s.求:
如图所示,质量mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B以初速度v0=10m/s沿水平方向向右运动,与A碰撞后都向右运动.木块A与挡板碰撞后立即反弹(设木块A与挡板碰撞过程无机械能损失).后来木块A与B发生二次碰撞,碰后A、B同向运动,速度大小分别为1m/s、4m/s.求:



 如图所示,竖直固定的足够长的光滑金属导轨MN、PQ,间距为l=0.2m,其电阻不计.完全相同的两金属棒ab、cd垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.01kg,电阻均为R=0.2Ω,棒cd放置在水平绝缘平台上,整个装置处在垂直于导轨平面向里的匀强磁场中,磁感应强度B=1.0T.棒ab在竖直向上的恒力F作用下由静止开始向上运动,当ab棒运动x=0.1m时达到最大速度vm,此时cd棒对绝缘平台的压力恰好为零.取g=10m/s2,求:
如图所示,竖直固定的足够长的光滑金属导轨MN、PQ,间距为l=0.2m,其电阻不计.完全相同的两金属棒ab、cd垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.01kg,电阻均为R=0.2Ω,棒cd放置在水平绝缘平台上,整个装置处在垂直于导轨平面向里的匀强磁场中,磁感应强度B=1.0T.棒ab在竖直向上的恒力F作用下由静止开始向上运动,当ab棒运动x=0.1m时达到最大速度vm,此时cd棒对绝缘平台的压力恰好为零.取g=10m/s2,求: 如图所示,在直角坐标系xOy平面内,第二象限中虚线MN平行于y轴,N点坐标为(-L,0),其左侧有水平向左的匀强电场E1,MN与y轴之间有沿y轴正方向的匀强电场E2,E1、E2均未知,在第一、三、四象限内有垂直纸面向里的匀强磁场,磁感应强度B未知.现有一质量为m、电荷量为q的负粒子从图中A点静止释放,不计粒子重力,粒子到达MN上的P点是速度为v0,速度方向水平,粒子从y轴上的C点(0,0.5L)与y轴负方向成30°角进入磁场,偏转后从x轴上的D点(图中未画出)垂直x轴穿出磁场并进入MN左侧电场且刚好又击中P点,求:
如图所示,在直角坐标系xOy平面内,第二象限中虚线MN平行于y轴,N点坐标为(-L,0),其左侧有水平向左的匀强电场E1,MN与y轴之间有沿y轴正方向的匀强电场E2,E1、E2均未知,在第一、三、四象限内有垂直纸面向里的匀强磁场,磁感应强度B未知.现有一质量为m、电荷量为q的负粒子从图中A点静止释放,不计粒子重力,粒子到达MN上的P点是速度为v0,速度方向水平,粒子从y轴上的C点(0,0.5L)与y轴负方向成30°角进入磁场,偏转后从x轴上的D点(图中未画出)垂直x轴穿出磁场并进入MN左侧电场且刚好又击中P点,求: