Question

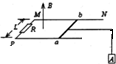如图所示，间距为L、电阻不计的两根平行金属导轨MN、PQ（足够长）被固定在同一水平面内，M、P间连接了一电阻R长度为L、质量为m、电阻也为R的导体棒ab垂直置于导轨上，一根轻绳绕过定滑轮后沿两金属导轨的中线与ab棒连接，其下端悬挂一个质量也为m的物体A，整个装置处于方向竖直向上、磁感应强度大小为B的匀强磁场中．开始时使导体棒ab和物体A都处于静止状态且轻绳拉直，现释放A，经过时间t，物体A下降的高度为h，速度为v．不计一切摩擦，导体棒始终与导轨接触良好，重力加速度为g．
求此时刻：
（1）a、b两端间的电压；
（2）物体A的加速度大小．

Answer 1

分析：（1）释放A后垂直切割磁感线，产生感应电动势，由E=BLv求出感应电动势，由欧姆定律可求出感应电流，并能得出a、b两端间的电压．
（2）由F=BIL求出棒ab所受的安培力大小，根据牛顿第二定律分别研究棒ab和A物体，可求解加速度．

解答：解：（1）t时刻，ab棒产生的感应电动势为 E=BLv，
回路中的感应电流：I=

E

2R

=

BLv

2R

则a、b两端间的电压为：U=IR=

1

2

BLv．
（2）设绳子的拉力大小为T，根据牛顿第二定律得，
  对ab棒：T-BIL=ma，
  对A：mg-T=ma
联立以上各式解得：a=

g

2

-

B2L2v

4mR

答：（1）a、b两端间的电压为

1

2

BLv；
（2）物体A的加速度大小为

g

2

-

B2L2v

4mR

．

点评：本题是电磁感应、电路、牛顿第二定律等知识的综合，对于连接体采用隔离法求解加速度，基本题．