题目内容
7. 两物块A、B用轻弹簧相连,质量均为2kg,最初,A、B两物块均以v=6m/s的速度在光滑水平面上向右匀速运动,质量4kg的物块C静止在A、B的正前方,其情景如图所示.B与C碰撞后二者会粘在一起运动.求在此后的运动中弹簧的最大弹性势能.
两物块A、B用轻弹簧相连,质量均为2kg,最初,A、B两物块均以v=6m/s的速度在光滑水平面上向右匀速运动,质量4kg的物块C静止在A、B的正前方,其情景如图所示.B与C碰撞后二者会粘在一起运动.求在此后的运动中弹簧的最大弹性势能.
分析 BC首先碰撞,粘在一起后再与A相互作用,当三者的速度相等时,AB间的距离最短,此时弹簧压缩量最大,此时弹簧的弹性势能最大,由动量守恒定律可求出此时三者的共同速度.
BC碰撞时,有机械能的损失,当BC粘在一起后与A相互作用的过程中,不但动量守恒,机械能也守恒,结合能量守恒可求系统中弹性势能的最大值.
解答 解:当A、B、C三者的速度相等时弹簧的弹性势能最大,设共同速度为${v}_{ABC}^{\;}$.由A、B、C三者组成的系统动量守恒得:
$({m}_{A}+{m}_{B})v=({m}_{A}+{m}_{B}+{m}_{C}){v}_{ABC}^{\;}$
解得:${v}_{ABC}^{\;}=\frac{(2+2)×6}{2+2+4}=3m/s$
B、C碰撞时B、C组成的系统动量守恒,设碰后瞬间B、C两者速度为${v}_{BC\;}^{\;}$,则有:
mBv=(mB+mC)${v}_{BC\;}^{\;}$
${v}_{BC\;}^{\;}$=$\frac{2×6}{2+4}$=2 m/s?
设物ABC速度相同时弹簧的弹性势能最大为Ep,根据能量守恒有:
Ep=$\frac{1}{2}$(mB+mC)${v}_{BC\;}^{2}$+$\frac{1}{2}$mAv2-$\frac{1}{2}$(mA+mB+mC)v2ABC=$\frac{1}{2}$×(2+4)×22+$\frac{1}{2}$×2×62-$\frac{1}{2}$×(2+2+4)×32=12 J
答:系统中弹性势能的最大值是12J
点评 该题考察了应用动量守恒定律和机械能守恒动量解决问题,但是要注意动量守恒时,机械能不一定守恒.该题的关键就是BC相互碰撞时动量守恒,但机械能不守恒,在BC粘在一起后再与A相互作用的过程中,不但动量守恒,机械能也守恒.

| A. | 波的图象表示介质中“某个质点”在“各个时刻”的位移 | |
| B. | 光的偏振现象说明光是横波 | |
| C. | 均匀变化的磁场产生均匀变化的电场,均匀变化的电场产生均匀变化的磁场 | |
| D. | 分别用红光和绿光在同一装置上进行双缝干涉实验,红光的干涉条纹间距较大 | |
| E. | 狭义相对论认为,在不同的惯性参考系中,一切物理规律都是相同的,真空中的光速也是相同的 |
 图示的木箱a用细线悬挂在天花板下,木箱内有用竖直弹簧相连的两物块b和c,b放于木箱的水平地板上.已知木箱a的质量为m,物块b的质量为2m,物块c的质量为3m,起初整个装置静止不动.用符号g表示重力加速度,针对剪断细线的瞬间,下列判断正确的是( )
图示的木箱a用细线悬挂在天花板下,木箱内有用竖直弹簧相连的两物块b和c,b放于木箱的水平地板上.已知木箱a的质量为m,物块b的质量为2m,物块c的质量为3m,起初整个装置静止不动.用符号g表示重力加速度,针对剪断细线的瞬间,下列判断正确的是( )| A. | 物块b下落的加速度为g | B. | 木箱a下落的加速度为2g | ||
| C. | 物块b对木箱底板的压力为mg | D. | 物块b对木箱底板的压力为2mg |
| A. | 进入加油站后,禁烟、禁火、禁打手机、严禁给塑料容器加注油品 | |
| B. | 滑动摩擦力可以对物体做正功,也可以对物体做负功,也可以对物体不做功 | |
| C. | 电荷在电势高的地方,电势能大,电荷在电势低的地方,电势能小 | |
| D. | 灵敏电流表在运输的时候应该用导线把两个接线柱连一起 |

| A. | 流过灯泡L的电流每秒钟方向改变50次 | |
| B. | 原线圈两端输入电压的瞬时值表达式为u=311sin(50 π t)(V) | |
| C. | 滑片P向下滑动的过程中,变压器的输入功率变小,V1表示数不变 | |
| D. | 滑片P向下滑动的过程中,灯泡L仍能正常发光,A1表示数变大,A2表示数变大 |
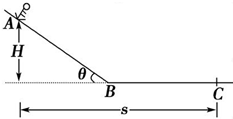 滑雪者从高为H的山坡上A点由静止下滑,到B点后又在水平雪面上滑行,最后停止在C点.A、C两点的水平距离为s,求滑雪板与雪面间的动摩擦因数μ.
滑雪者从高为H的山坡上A点由静止下滑,到B点后又在水平雪面上滑行,最后停止在C点.A、C两点的水平距离为s,求滑雪板与雪面间的动摩擦因数μ.
 为待接入的理想电压表.如果要求在测量中,风速从零开始增加,电压表的示数也从零开始增加,则电压表的“+”端和“-”端应分别连接到电路中的b点和d点(在“a”“b”“c”“d”中选填).
为待接入的理想电压表.如果要求在测量中,风速从零开始增加,电压表的示数也从零开始增加,则电压表的“+”端和“-”端应分别连接到电路中的b点和d点(在“a”“b”“c”“d”中选填). 如图甲所示,将长方形导线框abcd垂直磁场方向放入匀强磁场B中,规定垂直ab边向右为ab边所受安培力F的正方向,F随时间的变化关系如图乙所示.选取垂直纸面向里为磁感应强度B的正方向,不考虑线圈的形变,则B随时间t的变化关系不可能是下列选项中的( )
如图甲所示,将长方形导线框abcd垂直磁场方向放入匀强磁场B中,规定垂直ab边向右为ab边所受安培力F的正方向,F随时间的变化关系如图乙所示.选取垂直纸面向里为磁感应强度B的正方向,不考虑线圈的形变,则B随时间t的变化关系不可能是下列选项中的( )



 在绝缘水平面上方均匀分布着方向与水平向右成60°角斜向上的磁场中,一通有如图所示的恒定电流I的金属方棒,在安培力作用下水平向右做匀速直线运动.已知棒与水平面间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$.若在磁场方向由图示方向开始沿逆时针缓慢转动至竖直向上的过程中棒始终保持匀速直线运动,此过程中磁场方向与水平向右的夹角设为θ,则关于磁场的磁感应强度的大小B与θ的变化关系图象可能正确的是( )
在绝缘水平面上方均匀分布着方向与水平向右成60°角斜向上的磁场中,一通有如图所示的恒定电流I的金属方棒,在安培力作用下水平向右做匀速直线运动.已知棒与水平面间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$.若在磁场方向由图示方向开始沿逆时针缓慢转动至竖直向上的过程中棒始终保持匀速直线运动,此过程中磁场方向与水平向右的夹角设为θ,则关于磁场的磁感应强度的大小B与θ的变化关系图象可能正确的是( )


