题目内容
 原长分别为L1、L2,劲度系数分别为k1、k2的弹簧a、b,连接两个质量分别为m1、m2的大小不计的物体A、B,B放置于地面上,如图所示,现在a的上端作用一个大小变化的外力缓慢向上拉,直到B刚要离开地面,求此过程中:
原长分别为L1、L2,劲度系数分别为k1、k2的弹簧a、b,连接两个质量分别为m1、m2的大小不计的物体A、B,B放置于地面上,如图所示,现在a的上端作用一个大小变化的外力缓慢向上拉,直到B刚要离开地面,求此过程中:(1)A物体上端移动的距离
(2)弹簧a的上端移动的距离△x为多少?
分析:如图所示,弹簧a处于原长状态,弹力为零;弹簧b处于压缩状态,弹力大小与A物体的重力大小相等;当向上拉a使B刚要离开地面时,此时弹簧a处于拉伸状态,a中弹力大小为A、B两物体的重力之和,此时弹簧b处于拉伸状态,弹力大小为B物体的重力.根据胡克定律,可解得弹簧上端移动的距离△x.
解答:解:(1)初状态时,弹簧a处于原长状态,弹力为0;弹簧b处于压缩状态,令此时b压缩量为xb1,对A受力分析,

此时因A物体处于平衡状态,可知b弹力大小与A物体所受重力大小相等:
FbA=k2xb1
得:xb1=
B刚要离开地面时,设弹簧b的伸长量为xb2,对B而言:m2g=k2xb2
得:xb2=
A物体上端移动的距离:L=xb1+xb2=
(2)以AB物体整体为研究对象,设a弹簧的伸长量为xa,根据平衡条件:(m1+m2)g=k1xa
所以:xa=
;
弹簧a的上端上升的距离:△X=xb1+xb2+xa=
+
+
=
答:(1)A物体上端移动的距离为
.(2)弹簧a的上端移动的距离△X为
.

此时因A物体处于平衡状态,可知b弹力大小与A物体所受重力大小相等:
FbA=k2xb1
得:xb1=
| m1g |
| k2 |
B刚要离开地面时,设弹簧b的伸长量为xb2,对B而言:m2g=k2xb2
得:xb2=
| m2g |
| k2 |
A物体上端移动的距离:L=xb1+xb2=
| m1g+m2g |
| k2 |
(2)以AB物体整体为研究对象,设a弹簧的伸长量为xa,根据平衡条件:(m1+m2)g=k1xa
所以:xa=
| (m1+m2)g |
| k1 |
弹簧a的上端上升的距离:△X=xb1+xb2+xa=
| m1g |
| k2 |
| m2g |
| k2 |
| (m1+m2)g |
| k1 |
| (k1+k2)(m1+m2)g |
| k1k2 |
答:(1)A物体上端移动的距离为
| m1g+m2g |
| k2 |
| (k1+k2)(m1+m2)g |
| k1k2 |
点评:主要考查胡克定律的应用,弹簧拉伸和压缩时均遵循胡克定律,解题时注意对弹簧拉伸还是压缩的判断.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 如图所示,原长分别为L1和L2,劲度系数分别为k1、k2的轻弹簧竖直悬挂在天花板上,两弹簧之间有一质量为m1的物体,最下端挂着质量为m2的另一物体,整个装置处于静止状态,求:
如图所示,原长分别为L1和L2,劲度系数分别为k1、k2的轻弹簧竖直悬挂在天花板上,两弹簧之间有一质量为m1的物体,最下端挂着质量为m2的另一物体,整个装置处于静止状态,求: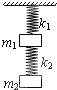 如图所示,原长分别为L1和L2、劲度系数分别为k1和k2的轻质弹簧竖直悬挂在天花板上.两弹簧之间有一质量为m1的物体,最下端挂着质量为m2的另一物体,整个装置处于静止状态.求这时两个弹簧的总长度为多大?
如图所示,原长分别为L1和L2、劲度系数分别为k1和k2的轻质弹簧竖直悬挂在天花板上.两弹簧之间有一质量为m1的物体,最下端挂着质量为m2的另一物体,整个装置处于静止状态.求这时两个弹簧的总长度为多大? 如图所示,原长分别为L1和L2、劲度系数分别为k1和k2的轻质弹簧竖直地悬挂在天花板下.两弹簧之间有一质量为m1物体,最下端挂着质量为m2的另一个物体,整个装置处于静止状态.现用一个质量为M的平板把下面的物体竖直缓慢地向上托起,直到两个弹簧的总长度等于两弹簧的原长之和,重力加速度为g,这时平板受到下面物体的压力大小等于( )
如图所示,原长分别为L1和L2、劲度系数分别为k1和k2的轻质弹簧竖直地悬挂在天花板下.两弹簧之间有一质量为m1物体,最下端挂着质量为m2的另一个物体,整个装置处于静止状态.现用一个质量为M的平板把下面的物体竖直缓慢地向上托起,直到两个弹簧的总长度等于两弹簧的原长之和,重力加速度为g,这时平板受到下面物体的压力大小等于( )